Classification (Regressions) V.S. Clustering

  • Classifications are supervised learning
  • Clustering are unsupervised learning

Cluster Analysis

Clustering is about grouping data points together based on similarities among them and difference from others.

Observations in a data set can be divided into different groups and sometimes this is very useful.

The goal of clustering:

  • to maximize the similarity of observations within a cluster
  • to maximize the dissimilarity between clusters

Cluster Analysis is a great starting point but rarely the sole method used for drawing conclusions.

Cluster Analysis don’t have labels. It is called unsupervised learning.

We cluster the observations in different groups but we have no clue if these clusters are.

The output we get is something that we must name ourselves.

Math Prerequisites

Euclidean distance

Euclidean distance is the distance Between Two Data Points.

When performing clustering we would be fighting the distance between clusters right.

Well if we work in n dimensional space we must know how to measure the distance.

section.

In 2D Space:

d=(x2−x1)2+(y2−y1)2d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}

In 3D space:

d=(x2−x1)2+(y2−y1)2+(z2−z1)2d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2+(z_2-z_1)^2}

Centroid

A centroid is the mean position of a group of points. (Aka center of mass)

Centroid of a triangle:

How to find Centroid for different shapes

In clustering, the centroid will be the mean position of many points.

Applications of Clustering

Clustering is often used as a preliminary step of all types of analysis.

Data Scientists often turn to it when they have no idea where to start.

There are many applications of clustering.

Market Segmentation

The firm gives you all the data they’ve gathered and give you the green light to create their next marketing campaign.

Using scatterplot, Cluster analysis allows you to identify four big clusters.

You can find the following clusters:

  • Young people who spend a lot
  • Young people who spend a little bit
  • Middle aged people who spend a lot
  • Middle aged people who don’t spend much

This Cluster analysis can help us to identify the target customers.

Image Segmentation

  • Colors can be clusters in an Image.
  • E.g. By reducing clusters, we can compress the image size (less colors)
  • Image Segmentation often applied to Object Recognition and Computer Vision

We will focus on Market Segmentation but not Image Segmentation in this section.

K-Means Clustering

Note: K-Means Clustering is a type of Flat Clustering.

There are different methods we can apply to identify clusters. The most popular one is K-Means.

K-means clustering: how it works

Key Steps:

  1. Choose the number of clusters (K)
  2. Specify the cluster seeds
  3. Assign each point to a centroid
  4. Adjust the centroids
  5. Repeat 3 and 4 until we can no longer reassign points

WCSS (within-cluster sum of squares)

WCSS is a measure developed within the ANOVA framework. It gives a very good idea about the different distance between different clusters and within clusters, thus providing us a rule for deciding the appropriate number of clusters.

Clustering is about:

  • minimizing the distance between points in a cluster (WCSS)
    • distance between points in a cluster is called WCSS (within-cluster sum of squares)
  • and maximizing the distance between clusters.

We want WCSS as low as possible.

Elbow Method

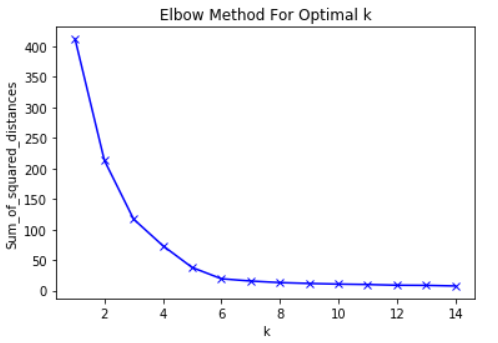
In cluster analysis, the elbow method is a heuristic used in determining the number of clusters in a data set. The method consists of plotting the explained variation as a function of the number of clusters, and picking the elbow of the curve as the number of clusters to use.

In this case the optimal clusters is 3, and 2 would be suboptimal.

Pros and Cons using K-Means

Pros :

  • Simple to understand
  • Fast to cluster
  • Widely available
  • Easy to implement
  • Always yields a result

Cons (and Remedies) :

  • Need to pick K (use the elbow method)
  • Sensitive to initialization (use k-means++)
  • Sensitive to outliers (just remove outliers)
  • Produces spherical solutions
  • Need to determine to use Standardization or not

K-Means Clustering in Python

We will be using sklearn.

Import the relevant libraries

1
2
3
4
5
6
7
8
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Set the styles to Seaborn
sns.set()
# Import the KMeans module so we can perform k-means clustering with sklearn
from sklearn.cluster import KMeans

Load the data

1
2
3
4
5
# Load the clusters data
data = pd.read_csv('clusters.csv')

# Check out the data manually 
data

Lets say we have this set of data.

^ Notice here Language is a Categorical Data. Thus we need to map the data.

Mapping Categoric Data

To map the data:

1
2
3
data_mapped = data.copy()
data_mapped['Language'] = data_mapped['Language'].map({'English':0,'French':1,'German':2})
data_mapped

Plot the data

1
2
3
4
5
6
7
# Use the simplest code possible to create a scatter plot using the longitude and latitude
# Note that in order to reach a result resembling the world map, we must use the longitude as y, and the latitude as x
plt.scatter(data['Longitude'],data['Latitude'])
# Set limits of the axes, again to resemble the world map
plt.xlim(-180,180)
plt.ylim(-90,90)
plt.show

Select the features

DataFrame.iloc(row indices, column indices) slice the data frame, given rows and columns to e kept.

Example 1: We select Latitude and Longitude in this case.

1
2
3
4
5
6
7
8
9
10
11
12
# iloc is a method used to 'slice' data 
# 'slice' is not technically correct as there are methods 'slice' which are a bit different
# The term used by pandas is 'selection by position'
# The first argument of identifies the rows we want to keep
# The second - the columns
# When choosing the columns, e.g. a:b, we will keep columns a,a+1,a+2,...,b-1 ; so column b is excluded
x = data.iloc[:,1:3]
# for this particular case, we are choosing columns 1 and 2
# Note column indices in Python start from 0

# Check if we worked correctly
x

Example2 : We select Language in this case.

1
2
3
x2 = data_mapped.iloc[:,3:4]

x2

Example3: We select all both Latitude, Longitude and Language.

1
2
3
x3 = data_mapped.iloc[:,1:4]

x3

Clustering

1
2
3
4
5
6
7
8
9
10
11
# Create an object (which we would call kmeans)
# The number in the brackets is K, or the number of clusters we are aiming for
kmeans = KMeans(3)
# e.g. If you want 7 clusters,
# kmeans = KMeans(7)


# Fit the input data, i.e. cluster the data in X in K clusters
kmeans.fit(x)
#kmeans.fit(x2)
#kmeans.fit(x3)

Show the Clustering results

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Create a variable which will contain the predicted clusters for each observation
identified_clusters = kmeans.fit_predict(x)
#identified_clusters = kmeans.fit_predict(x2)
#identified_clusters = kmeans.fit_predict(x3)


# Check the result
identified_clusters

# Create a copy of the data
data_with_clusters = data.copy()
# Create a new Series, containing the identified cluster for each observation
data_with_clusters['Cluster'] = identified_clusters
# Check the result
data_with_clusters

Then plot the scatter plot

1
2
3
4
5
6
7
8
9
# Plot the data using the longitude and the latitude
# c (color) is an argument which could be coded with a variable 
# The variable in this case has values 0,1,2, indicating to plt.scatter, that there are three colors (0,1,2)
# All points in cluster 0 will be the same colour, all points in cluster 1 - another one, etc.
# cmap is the color map. Rainbow is a nice one, but you can check others here: https://matplotlib.org/users/colormaps.html
plt.scatter(data_with_clusters['Longitude'],data_with_clusters['Latitude'],c=data_with_clusters['Cluster'],cmap='rainbow')
plt.xlim(-180,180)
plt.ylim(-90,90)
plt.show()

Selecting the number of clusters

WCSS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Get the WCSS for the current solution
kmeans.inertia_

# Create an empty list
wcss=[]

# Create all possible cluster solutions with a loop
for i in range(1,7):
    # Cluster solution with i clusters
    kmeans = KMeans(i)
    # Fit the data
    kmeans.fit(x)
    # Find WCSS for the current iteration
    wcss_iter = kmeans.inertia_
    # Append the value to the WCSS list
    wcss.append(wcss_iter)
    
# Let's see what we got
wcss

Elbow Method

1
2
3
4
5
6
7
8
9
10
# Create a variable containing the numbers from 1 to 6, so we can use it as X axis of the future plot
number_clusters = range(1,7)
# Plot the number of clusters vs WCSS
plt.plot(number_clusters,wcss)
# Name your graph
plt.title('The Elbow Method')
# Name the x-axis
plt.xlabel('Number of clusters')
# Name the y-axis
plt.ylabel('Within-cluster Sum of Squares')

K-Means Clustering in Python (Full Example)

In this example, I will be using the Iris flower dataset.

The Iris flower dataset is one of the most popular ones for machine learning. You can read a lot about it online and have probably already heard of it: https://en.wikipedia.org/wiki/Iris_flower_data_set

Import the relevant libraries

1
2
3
4
5
6
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.cluster import KMeans

Load the data

Load data from the csv file: ‘iris_dataset.csv’.

1
2
3
4
# Load the data
data = pd.read_csv('iris-dataset.csv')
# Check the data
data

Plot the data

Try to cluster the iris flowers by the shape of their sepal.

Hint: Use the ‘sepal_length’ and ‘sepal_width’ variables.

1
2
3
4
5
6
# Create a scatter plot based on two corresponding features (sepal_length and sepal_width; OR petal_length and petal_width)
plt.scatter(data['sepal_length'],data['sepal_width'])
# Name your axes
plt.xlabel('Lenght of sepal')
plt.ylabel('Width of sepal')
plt.show()

Clustering (unscaled data)

Separate the original data into 2 clusters.

1
2
3
4
5
6
# create a variable which will contain the data for the clustering
x = data.copy()
# create a k-means object with 2 clusters
kmeans = KMeans(2)
# fit the data
kmeans.fit(x)
1
2
3
4
# create a copy of data, so we can see the clusters next to the original data
clusters = data.copy()
# predict the cluster for each observation
clusters['cluster_pred']=kmeans.fit_predict(x)
1
2
# create a scatter plot based on two corresponding features (sepal_length and sepal_width; OR petal_length and petal_width)
plt.scatter(clusters['sepal_length'], clusters['sepal_width'], c= clusters ['cluster_pred'], cmap = 'rainbow')

Standardize the variables (Scaling Data)

Import and use the scale function from sklearn to standardize the data.

1
2
3
4
5
6
# import some preprocessing module
from sklearn import preprocessing

# scale the data for better results
x_scaled = preprocessing.scale(data)
x_scaled

Clustering (scaled data)

1
2
3
4
# create a k-means object with 2 clusters
kmeans_scaled = KMeans(2)
# fit the data
kmeans_scaled.fit(x_scaled)
1
2
3
4
# create a copy of data, so we can see the clusters next to the original data
clusters_scaled = data.copy()
# predict the cluster for each observation
clusters_scaled['cluster_pred']=kmeans_scaled.fit_predict(x_scaled)
1
2
# create a scatter plot based on two corresponding features (sepal_length and sepal_width; OR petal_length and petal_width)
plt.scatter(clusters_scaled['sepal_length'], clusters_scaled['sepal_width'], c= clusters_scaled ['cluster_pred'], cmap = 'rainbow')

Take Advantage of the Elbow Method

WCSS

1
2
3
4
5
6
7
8
9
wcss = []
# 'cl_num' is a that keeps track the highest number of clusters we want to use the WCSS method for. We have it set at 10 right now, but it is completely arbitrary.
cl_num = 10
for i in range (1,cl_num):
    kmeans= KMeans(i)
    kmeans.fit(x_scaled)
    wcss_iter = kmeans.inertia_
    wcss.append(wcss_iter)
wcss

The Elbow Method

1
2
3
4
5
number_clusters = range(1,cl_num)
plt.plot(number_clusters, wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Within-cluster Sum of Squares')

Based on the Elbow Curve, plot several graphs with the appropriate amounts of clusters you believe would best fit the data.

Understanding the Elbow Curve

Construct and compare the scatter plots to determine which number of clusters is appropriate for further use in our analysis. Based on the Elbow Curve, 2, 3 or 5 seem the most likely.

2 clusters

Start by seperating the standardized data into 2 clusters.

1
2
kmeans_2 = KMeans(2)
kmeans_2.fit(x_scaled)

Construct a scatter plot of the original data using the standartized clusters.

1
2
3
# Remember that we are plotting the non-standardized values of the sepal length and width. 
clusters_2 = x.copy()
clusters_2['cluster_pred']=kmeans_2.fit_predict(x_scaled)
1
plt.scatter(clusters_2['sepal_length'], clusters_2['sepal_width'], c= clusters_2 ['cluster_pred'], cmap = 'rainbow')

3 Clusters

Redo the same for 3 and 5 clusters.

1
2
kmeans_3 = KMeans(3)
kmeans_3.fit(x_scaled)
1
2
clusters_3 = x.copy()
clusters_3['cluster_pred']=kmeans_3.fit_predict(x_scaled)
1
plt.scatter(clusters_3['sepal_length'], clusters_3['sepal_width'], c= clusters_3 ['cluster_pred'], cmap = 'rainbow')

5 Clusters

1
2
kmeans_5 = KMeans(5)
kmeans_5.fit(x_scaled)
1
2
clusters_5 = x.copy()
clusters_5['cluster_pred']=kmeans_5.fit_predict(x_scaled)
1
plt.scatter(clusters_5['sepal_length'], clusters_5['sepal_width'], c= clusters_5 ['cluster_pred'], cmap = 'rainbow')

Compare your solutions to the original iris dataset

The original (full) iris data is located in iris-with-answers.csv. Load the csv, plot the data and compare it with your solution.

Obviously there are only 3 species of Iris, because that’s the original (truthful) iris dataset.

The 2-cluster solution seemed good, but in real life the iris dataset has 3 SPECIES (a 3-cluster solution).

Therefore, clustering cannot be trusted at all times. Sometimes it seems like x clusters are a good solution, but in real life, there are more (or less).

1
real_data = pd.read_csv('iris-with-answers.csv')
1
real_data['species'].unique()

output: array(['setosa', 'versicolor', 'virginica'], dtype=object)

1
2
# We use the map function to change any 'yes' values to 1 and 'no'values to 0. 
real_data['species'] = real_data['species'].map({'setosa':0, 'versicolor':1 , 'virginica':2})
1
real_data.head()

Scatter plots (which we will use for comparison)

‘Real data’

Looking at the first graph it seems like the clustering solution is much more intertwined than what we imagined (and what we found before)

1
plt.scatter(real_data['sepal_length'], real_data['sepal_width'], c= real_data ['species'], cmap = 'rainbow')

Examining the other scatter plot (petal length vs petal width), we see that in fact the features which actually make the species different are petals and NOT sepals!

Note that ‘real data’ is the data observed in the real world (biological data)

1
plt.scatter(real_data['petal_length'], real_data['petal_width'], c= real_data ['species'], cmap = 'rainbow')

Our clustering solution data

It seems that our solution takes into account mainly the sepal features

1
plt.scatter(clusters_3['sepal_length'], clusters_3['sepal_width'], c= clusters_3 ['cluster_pred'], cmap = 'rainbow')

Instead of the petals…

1
plt.scatter(clusters_3['petal_length'], clusters_3['petal_width'], c= clusters_3 ['cluster_pred'], cmap = 'rainbow')

Further clarifications

In fact, if you read about it, the original dataset has 3 sub-species of the Iris flower. Therefore, the number of clusters is 3.

This shows us that:

  • the Eblow method is imperfect (we might have opted for 2 or even 4)
  • k-means is very useful in moments where we already know the number of clusters - in this case: 3
  • biology cannot be always quantified (or better)… quantified with k-means! Other methods are much better at that

Finally, you can try to classify them (instead of cluster them, now that you have all the data)!

Hierarchical Clustering

There are two types of Hierarchical Clustering:

  • Agglomerative (Bottom-up)
    • each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy, until all observations are in a single cluster.
  • Divisive (Top-down)
    • all observations are in the same cluster and then split into smaller clusters.
    • To find the best split we must explore all possibilities at each step. (Elbow Methods)

We will focus on Agglomerative Clustering.

Agglomerative

Each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy, until all observations are in a single cluster.

Dendrogram

The Agglomerative Graph is called Dendrogram.

In above example, 6 clusters -> 5 clusters left (Germany and France merged) -> 4 (UK and Germany and France merged) -> 3 (Canada and USA merged) -> 2 (UK and Germany and France and Canada and USA merged) -> 1 cluster in the end (Merge with Australia).

Note: All cluster solutions are nested inside the Dendrogram.

Pros of Dendrogram

  • Hierarchical clustering shows all the possible linkages between clusters
  • We understand the data much, much better
  • No need to preset the number of clusters (like with k-means)
  • Many methods the perform hierarchiclal clustering

Cons of Dendrogram

  • Huge scaled obbservations will be extremely hard to be examined

HeatMap

Heatmap uses colors to represent a value.

Choosing the coolest cmap

Dendrogram and Heatmap in Python

Import the relevant libraries

1
2
3
4
import numpy as np
import pandas as pd
import seaborn as sns
# We don't need matplotlib this time

Load the data

pd.read_csv(*.csv,index_col) loads a given CSV file as a data frame; index_col is an argument which can specify a given column from the CSV as index of the data frame.

1
2
3
4
# Load the standardized data
# index_col is an argument we can set to one of the columns
# this will cause one of the Series to become the index
data = pd.read_csv('Country clusters standardized.csv', index_col='Country')
1
2
3
4
5
6
7
# Create a new data frame for the inputs, so we can clean it
x_scaled = data.copy()
# Drop the variables that are unnecessary for this solution
x_scaled = x_scaled.drop(['Language'],axis=1)

# Check what's inside
x_scaled

Plot the data

1
2
# Using the Seaborn method 'clustermap' we can get a heatmap and dendrograms for both the observations and the features
sns.clustermap(x_scaled, cmap='mako')

Choosing the coolest cmap

Reference

The Data Science Course 2020: Complete Data Science Bootcamp