Logistic Regression Assumption

We should consider them before performing Logistic regression analysis.

  • No endogeneity of regressor
  • Normality and homoscedasticity
  • No autocorrelation
  • No multicollinearity

We should not violate the assumptions.

If a regression assumption is violated, performing regression analysis will yeild an incorrect result.

Logistic Regression

On real world problems often require more sophisticated non-linear models.

on-linear models can be :

  • Quadratic
  • Exponential
  • Logistic

Logistic Regression Model

A logistic regression implies that the possible outcomes are not numerical but rather categorical.

E.g. We can use logistic regression to predict Yes / No (Binary Prediction)

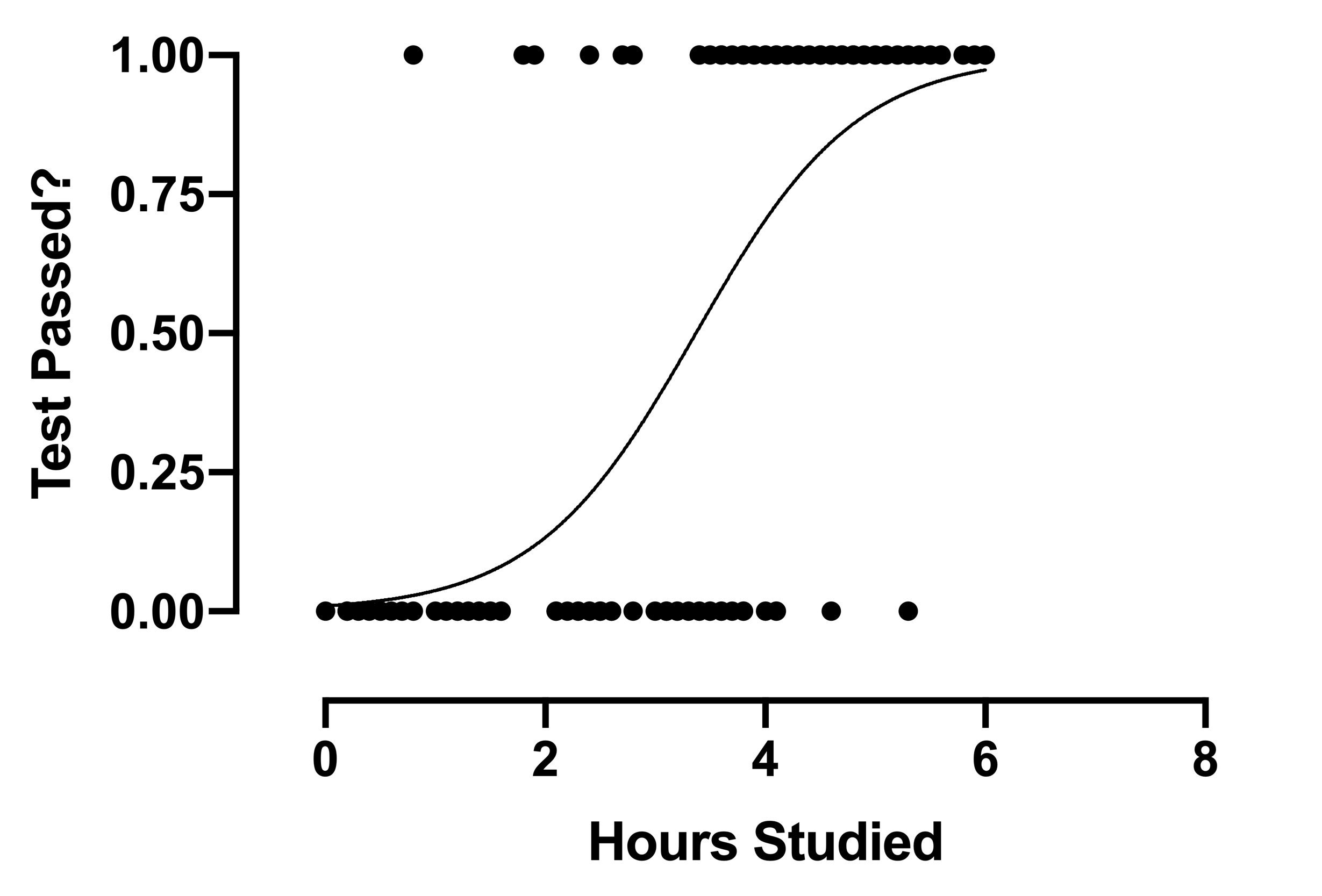
  • Logistic regression predicts the probability of an event occurring.
    • Input => Probability

Logistic Regression Equations

Logistic Regression Equation

p(Y)=e(β0+β1x1+⋯+βkxk)1+e(β0+β1x1+⋯+βkxk)p(Y)=\frac{e^{\left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)}}{1+e^{\left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)}}

Logit Regression Equation

p(Y)1−p(Y)=e(β0+β1x1+⋯+βkxk)\frac{p(Y)}{1-p(Y)}=e^{\left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)}

Odds and Binary Predictors

Note: Odds = p(Y)1−p(Y)\frac{p(Y)}{1-p(Y)}

log⁡(odds)=β0+β1x1+⋯+βkxk\log (o d d s)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}

In simplifier explaination,

log(odds)log(odds) = coef_of_const + coef_of_x1 ×x1+⋯\times x1 + \cdots

Note :

Difference of cc unit of x1x1:

log(odds2odds1)log(\frac{odds_2}{odds_1}) = coef_of_x1 (x12−x11)(x1_2 - x1_1)

Then

odds2=odds1×odds_2 = odds_1\times e^{coef_of_x1(x1_2 - x1_1)}

When x1 increases by cc, the odds of y increases by (odds2−100%odds_2 - 100\%).

The General Rule:

The change in the odds equals the exponential of the coefficient.

Δodds=ebk\Delta \mathrm{odd} \mathrm{s}=e^{b_{k}}

Example of Binary Predictors:

x1 will be only 1 or 0.

log(odds2odds1)log(\frac{odds_2}{odds_1}) = coef_of_x1(1−0)(1 - 0) = coef_of_x1

By taking exponent you can find the difference of odds1odds_1 and odds2odds_2 using numpy.

1
np.exp(coef_of_x1)

Then

odds2odds_2 = np.exp(coef_of_x1) ×odds1\times odds_1

You can say:

Given the same x1, 22 has np.exp(coef_of_x1) times higher oddeds to get yy.

Logistic Regression In Python (with StatsModels)

Import the relevant libraries

1
2
3
4
5
6
7
8
9
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# quickfix for statmodels library incase there is error
from scipy import stats
stats.chisqprob = lambda chisq, df: stats.chi2.sf(chisq, df)

Load the Data

Just like the same old ways

1
2
raw_data = pd.read_csv('xxxyyy.csv')
raw_data

Making Dummy variables by mapping all the entries

1
2
3
4
5
6
7
8
9
# We make sure to create a copy of the data before we start altering it. Note that we don't change the original data we loaded.
data = raw_data.copy()

# Removes the index column thata comes with the data
data = data.drop(['Unnamed: 0'], axis = 1)

# We use the map function to change any 'yes' values to 1 and 'no'values to 0. 
data['y'] = data['y'].map({'yes':1, 'no':0})
data

Declare the dependent and independent variables

1
2
3
y = data['y']
# x1 = data['x']
x1 = data[['x1','x2']]

Run the Regression

Just like before, we need to add constant

1
2
3
4
5
6
7
8
x = sm.add_constant(x1)
reg_log = sm.Logit(y,x)	# We use sm.Logit
results_log = reg_log.fit()
# ^ Output will tell the function value and Iterations.
# ^ It is possible that it won't learn.

# Get the regression summary
results_log.summary()

New Terms in Logistic Regression summary

  • MLE (Maximum likelihood estimation)
    • The bigger the likelihood function, the higher probability that our model is correct
  • Log-Likelihood
    • Value of the Log-Likelihood is usually negative
    • bigger Log-Likelihood is better
  • LL-Null (Log-Likelihood-null)
    • the log-likelihood of a model which has no independent variables
    • y=β0y = \beta_0
    • you may want to compare the log likelihood of your model with the LL-Null to see if your model has any explanatory power.
  • Pseudo R-squared: McFadden’s R-squared
    • A good pseudo r-squared is somewhere between 0.2 and 0.4.
    • this measure is mostly useful for comparing variations of the same model.
    • Different models will have completely different an incomparable pseudo r-squares.
  • P-values
    • Check if the model is significant and the variable is significant.

Accuracy

sm.LogitResults.predict() returns the values predicted by our model.

1
2
3
4
5
#apply formatting
np.set_printoptions(formatter={'float': lambda x: "{0:0.2f}".format(x)})

# SHOW PREDICTED VALUES
results_log.predict()

Output will show the p(Y)p(Y). I need to round the values to 0 or 1.

Now we show the actual values.

1
np.array(data['y'])
  • If 80% of the predicted values coincide with the actual values, we say the model has 80% accuracy.

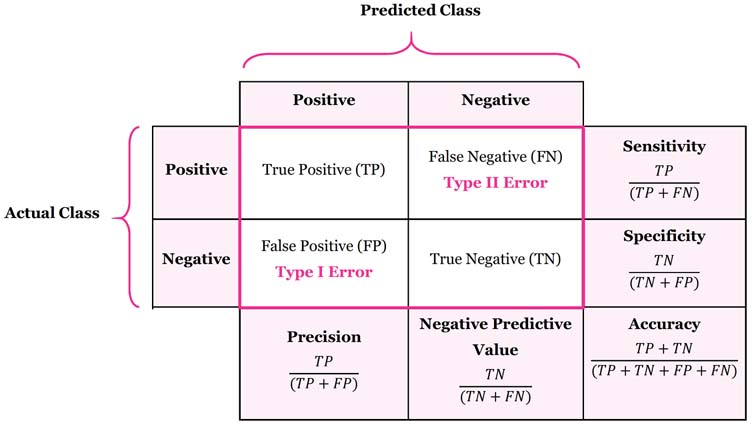
We dont need to compare the tables by ourselfs, just code it into Confusion Matrix.

sm.LogitResults.pred_table()

1
2
3
4
5
6
7
results_log.pred_table()

#format it as confusion matrix
cm_df = pd.DataFrame(results_log.pred_table())
cm_df.columns = ['Predicted 0', 'Predicted 1']
cm_df = cm_df.rename(index ={0: 'Actual 0', 1: 'Actual 1'})
cm_df

cm_df (Confusion Matrix DataFrame) may look like this:

In this table:

In 159 cases the model did the job well

  • For 69 observations the model predicted 0 and the true value was 0 (True Positive)
  • For 90 observations the model predicted 1 and the true value was 1 (True Negative)

In 9 cases the model got confused

  • For 4 observations the model predicted 0 and the true value was 1 (Type I Error)
  • For 5 observations the model predicted 1 and the true value was 0 (Type II Error)

Overall the model made an accurate prediction in 159 out of 168 cases = 94.6% accuracy

1
2
3
4
# Find the accuracy
cm = np.array(cm_df)
accuracy_train = (cm[0,0] + cm[1,1])/cm.sum()
accuracy_train

How to check the matrix

Data Science and Machine Learning : Confusion Matrix

Test the model using new data

Use our model to make predictions based on the test data

Load the test dataset

1
2
3
# Load the test dataset
test = pd.read_csv('xxxyyy_test.csv')
test
1
2
3
4
5
# Map the test data as you did with the train data
test['y'] = test['y'].map({'Yes': 1, 'No': 0})
test['x'] = test['x'].map({'Female': 1, 'Male': 0})
test
x # check the order

Remember:

our test data shape should look the same as the input data on which the regression was trained.

order is very important because the coefficients of the regression will expect it.

1
2
3
4
5
6
# Get the actual values (true values ; targets)
test_actual = test['y']
# Prepare the test data to be predicted
test_data = test.drop(['y'],axis=1)
test_data = sm.add_constant(test_data)
test_data

Now test_data will look exactly as x.

Now Create a confusion matrix and calculate the accuracy again.

We write our Confusion Matrix function.

Confusion Matrix shows how confused our model is

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def confusion_matrix(data,actual_values,model):
        
        # Confusion matrix 
        
        # Parameters
        # ----------
        # data: data frame or array
            # data is a data frame formatted in the same way as your input data (without the actual values)
            # e.g. const, var1, var2, etc. Order is very important!
        # actual_values: data frame or array
            # These are the actual values from the test_data
            # In the case of a logistic regression, it should be a single column with 0s and 1s
            
        # model: a LogitResults object
            # this is the variable where you have the fitted model 
            # e.g. results_log in this course
        # ----------
        
        #Predict the values using the Logit model
        pred_values = model.predict(data)
        # Specify the bins 
        bins=np.array([0,0.5,1])
        # Create a histogram, where if values are between 0 and 0.5 tell will be considered 0
        # if they are between 0.5 and 1, they will be considered 1
        cm = np.histogram2d(actual_values, pred_values, bins=bins)[0]
        # Calculate the accuracy
        accuracy = (cm[0,0]+cm[1,1])/cm.sum()
        # Return the confusion matrix and 
        return cm, accuracy

Usage

1
2
3
4
5
# Create a confusion matrix with the test data
cm = confusion_matrix(test_data,test_actual,results_log)
cm 
# left part is the confusion matrix
# the right value is the accuracy

Almost always the training accuracy is higher than the test accuracy. (Overfitting)

Lastly change it into DataFrame.

1
2
3
4
cm_df = pd.DataFrame(cm[0])
cm_df.columns = ['Predicted 0', 'Predicted 1']
cm_df = cm_df.rename(index ={0: 'Actual 0', 1: 'Actual 1'})
cm_df
  • Missclassification rate = 1 - accuracy

Reference

The Data Science Course 2020: Complete Data Science Bootcamp