Big O Notation

  • The Big O notation estimates the execution time of an algorithm in relation to the input size.

Best, Worst, and Average Cases

Best-case is not representative.

Worst-case is not representative, but worst-case analysis is very useful. You can show that the algorithm will never be slower than the worst-case.

Average-case analysis is ideal, but difficult to perform, because it is hard to determine the relative probabilities and distributions of various input instances for many problems.

Determining Big O Notation

Ignoring Multiplicative Constants

Algorithm analysis is focused on growth rate. The multiplicative constants have no impact on growth rates.

O(n/2) = O(100n) = O(n)

They are all the same so can be represented as O(n).

Ignoring Non-Dominating Terms

Algorithm analysis is for large input size. If the input size is small, there is no significance to estimate an algorithm’s efficiency.

O(n-1) = O(n)

Common Big O Notation

Constant Time

O(1)

  • If the time is not related to the input size, the algorithm is said to take constant time with the notation O(1).

Quadratic Time

O(n^2)

  • If you double the input size, the time for the algorithm is quadrupled.
  • Algorithms with a nested loop are often quadratic.

Logarithmic Time

O(log n)

  • The base of the log is 2, but the base does not affect a logarithmic growth rate, so it can be omitted.
  • The logarithmic algorithm grows slowly as the problem size increases.
  • If you square the input size, you only double the time for the algorithm.

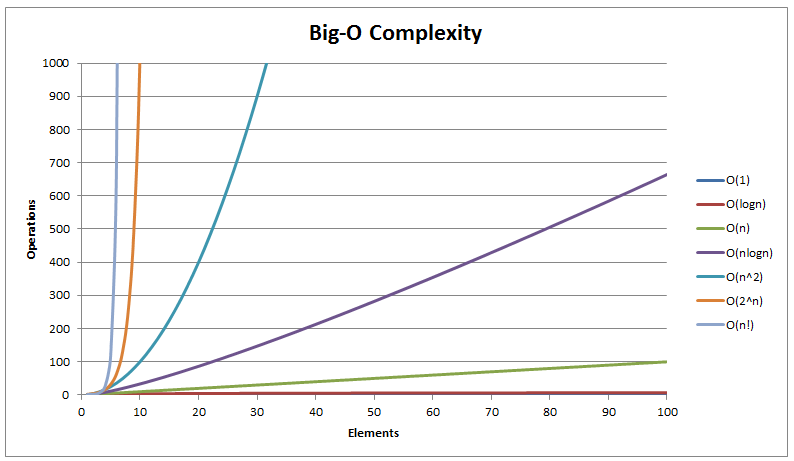
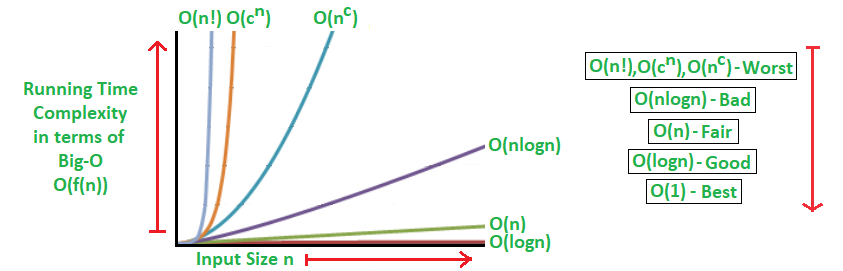
Comparing Common Growth Functions

O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n)

Sorting

Why study sorting?

  • sorting algorithms illustrate many creative approaches to problem solving and these approaches can be applied to solve other problems.
  • sorting algorithms are good for practicing fundamental programming techniques using selection statements, loops, methods, and arrays.
  • sorting algorithms are excellent examples to demonstrate algorithm performance.

Visualgo to Visualize Sorting Algorithms

Interactive Sorting Animation

Insertion Sort and Bubble Sort

Both Done by Swaping

Insertion Sort

  • Done by swaping adjacently
    • put the number at i into correct order by “inserting”

Best Case of Bubble Sort: O(n)

Worse Case of Bubble Sort: O(n^2)

Average Case of Bubble Sort: O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*Function to sort array using insertion sort*/
void sort(int arr[]) 
{ 
    int n = arr.length; 
    for (int i = 1; i < n; ++i) { 
        int key = arr[i]; 
        int j = i - 1; 
  
        /* Move elements of arr[0..i-1], that are 
           greater than key, to one position ahead 
           of their current position */
        while (j >= 0 && arr[j] > key) { 
            arr[j + 1] = arr[j]; 
            j = j - 1; 
        } 
        arr[j + 1] = key; 
    } 
}

Best Case of Insertion Sort: O(n)

Worse Case of Insertion Sort: O(n^2)

Average Case of Insertion Sort: O(n^2)

Bubble Sort

  • Done by swaping adjacently
    • Each iteration check number at i and number at i+1
      • swap them if the it is not in order

Insertion Sort vs Bubble Sort

Merge Sort and Quick Sort

Both done by Divide and Conquer.

Merge Sort

Merge Sort is a Divide and Conquer Algorithm.

  • Keep Dividing the Array into 2 parts until the array size become 1.
  • After Dividing them to smallest size, merging start.
  • Merging based on compasion of elements

Best Case of Merge Sort: O(n log n)

Worse Case of Merge Sort: O(n log n)

Average Case of Merge Sort: O(n log n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

// Merges two subarrays of arr[]. 
// First subarray is arr[l..m] 
// Second subarray is arr[m+1..r] 
void merge(int arr[], int l, int m, int r) 
{ 
    // Find sizes of two subarrays to be merged 
    int n1 = m - l + 1; 
    int n2 = r - m; 
  
    /* Create temp arrays */
    int L[] = new int [n1]; 
    int R[] = new int [n2]; 
  
    /*Copy data to temp arrays*/
    for (int i=0; i<n1; ++i) 
        L[i] = arr[l + i]; 
    for (int j=0; j<n2; ++j) 
        R[j] = arr[m + 1+ j]; 
  
  
    /* Merge the temp arrays */
  
    // Initial indexes of first and second subarrays 
    int i = 0, j = 0; 
  
    // Initial index of merged subarry array 
    int k = l; 
    while (i < n1 && j < n2) 
    { 
        if (L[i] <= R[j]) 
        { 
            arr[k] = L[i]; 
            i++; 
        } 
        else
        { 
            arr[k] = R[j]; 
            j++; 
        } 
        k++; 
    } 
  
    /* Copy remaining elements of L[] if any */
    while (i < n1) 
    { 
        arr[k] = L[i]; 
        i++; 
        k++; 
    } 
  
    /* Copy remaining elements of R[] if any */
    while (j < n2) 
    { 
        arr[k] = R[j]; 
        j++; 
        k++; 
    } 
} 
  
// Main function that sorts arr[l..r] using 
// merge() 
void sort(int arr[], int l, int r) 
{ 
    if (l < r) 
    { 
        // Find the middle point 
        int m = (l+r)/2; 
  
        // Sort first and second halves 
        sort(arr, l, m); 
        sort(arr , m+1, r); 
  
        // Merge the sorted halves 
        merge(arr, l, m, r); 
    } 
}

Quick Sort

  • Pivot divide array into 2 halfs
  • A pivot can be chosen arbitrarily.
  • A pivot divides a list into two sublists,
    • the elements in the first list are smaller than the pivot
    • the elements in the second list are larger than the pivot.

If two subpivot is not meeting the requirement (i.e. low is not < pivot, high is not > pivot), Swap them

When low subpivot and high subpivot is pointing to same number, from now on we need a new partition. We swap high subpivot with pivot when high subpivot is lower than pivot.

Quick Sort Partition Animation

https://stackoverflow.com/questions/6740183/quicksort-with-first-element-as-pivot-example

For example: make a first partition

5 2 9 3 8 4 0 1 6 7 (using first element 5 as pivot)

firstly, subpivot low is 2 while subpivot high is 7.

2 < 5 and 7 > 5 therefore both low and high subpivot point to next number (that is 9 and 6).

9 is not < 5 and 6 > 5, therefore low subpivot stops, high subpivot point to next number (that is 1).

1 is not > 5, In this moment the numbers in both subpivot swaps (1 and 9).

5 2 1 3 8 4 0 9 6 7

subpivot further moves. Both low and high subpivot is now point to next number (that is 3 and 0).

3 < 5 and 0 is not > 5, therefore high subpivot stops, low subpivot point to next number (that is 8).

8 is not < 5, In this moment the numbers in both subpivot swaps (8 and 0).

5 2 1 3 0 4 8 9 6 7

subpivot further moves. Both low and high subpivot is now point to next number (that is 4 and 4).

Since now the low subpivot and high subpivot is pointing to same number, from now on we need a new partition. We swap high subpivot with pivot when high subpivot is lower than pivot.

4 is not > 5, therefore high subpivot stops. the number of high subpivot and pivot are swapped.

Note the pivot is still pointing at 5.

4 2 1 3 0 5 8 9 6 7

Best Case of Quick Sort: O(n log n)

Worse Case of Quick Sort: O(n^2)

Average Case of Quick Sort: O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

/* This function takes last element as pivot, 
   places the pivot element at its correct 
   position in sorted array, and places all 
   smaller (smaller than pivot) to left of 
   pivot and all greater elements to right 
   of pivot */
int partition(int arr[], int low, int high) 
{ 
    int pivot = arr[high];  
    int i = (low-1); // index of smaller element 
    for (int j=low; j<high; j++) 
    { 
        // If current element is smaller than the pivot 
        if (arr[j] < pivot) 
        { 
            i++; 
  
            // swap arr[i] and arr[j] 
            int temp = arr[i]; 
            arr[i] = arr[j]; 
            arr[j] = temp; 
        } 
    } 
  
    // swap arr[i+1] and arr[high] (or pivot) 
    int temp = arr[i+1]; 
    arr[i+1] = arr[high]; 
    arr[high] = temp; 
  
    return i+1; 
} 
  
  
/* The main function that implements QuickSort() 
  arr[] --> Array to be sorted, 
  low  --> Starting index, 
  high  --> Ending index */
void sort(int arr[], int low, int high) 
{ 
    if (low < high) 
    { 
        /* pi is partitioning index, arr[pi] is  
          now at right place */
        int pi = partition(arr, low, high); 
  
        // Recursively sort elements before 
        // partition and after partition 
        sort(arr, low, pi-1); 
        sort(arr, pi+1, high); 
    } 
}

Merge Sort vs Quick Sort