Digital Signals and System [3] - Discrete-time Fourier

Keyword/Relationship Explained

For periodic signal, Signals can be constructed by summing sinusoids of different frequencies, amplitudes and phases.

Signals = $A_{0}+A_{1}cos(2\pi f_{1}t + \theta_{1})+A_{2}cos(2\pi f_{2}t + \theta_{2})+A_{3}cos(2\pi f_{3}t + \theta_{3})+...$

Waveform : a plot of a function of time

Spectrum : a plot of a function of frequency

Amplitude spectrum is even, while phase spectrum is odd.

Frequency-domain representation: Represented with the set of scaling factors + phase angles.

Frequency domain analysis = get the scaling factors and the phase angles ($A_i$ and $\theta_i$ )

We use different approaches for different signals.

Signal	Approach
Periodic continuous time signal	Continuous time Fourier Series (CTFS)
Aperiodic continuous time signal	Continuous time Fourier Transform (CTFT)
Periodic discrete time signal	Discrete time Fourier series (DTFS)
Aperiodic discrete time signal	Discrete time Fourier Transform (DTFT)

For continuous time signal, refer to here

Discrete-time Fourier Series (DTFS)

Used to analyze a periodic discrete-time signal

• Discrete time, discrete frequency
• Periodic in time, periodic in frequency

Definition

Inverse DTFS (for getting the x[n])

x[n]: periodic, n ={0, 1, …, N-1} is time index

N is period of the input signal.

$$X[k] \longrightarrow x[n]=\sum_{k=0}^{N-1} X[k] e^{j 2 \pi \frac{k n}{N}}$$

Forward DTFS (for getting the X[k])

X[k]: periodic, k={0, 1, …, N-1} is frequency index

N is period of the input signal.

$$x[n] \longrightarrow X[k]=\frac{1}{N} \sum_{n=0}^{N-1} x[n] e^{-j 2 \pi \frac{k n}{N}}$$

Properties of DTFS

Time shifting

A shift doesn’t affect the amplitude spectrum but the phase spectrum.

$$x\left[n-n_{0}\right] \longleftrightarrow e^{-j 2 \pi k \frac{n_{0}}{N}} X[k]$$

Frequency Shifting (Harmonic Number Shifting)

$$e^{j 2 \pi k_{0} \frac{n}{N}} x[n] \longleftrightarrow X\left[k-k_{0}\right]$$

Conjugation

$$x^{*}[n] \longleftrightarrow X^{*}[-k]$$

If $x[n]$ is a real-value sequence

• $x[n] = x^*[n] \rightarrow X[k] = X^*[-k]$
  • $|X[k]| = |X^*[-k]| = |X[-k]|$ -> Amplitude spectrum is an even function
  • $\angle X[k] = \angle X^*[-k] = -\angle X[-k]$ -> Phase spectrum is an odd function

Time Reversal

$$x[-n] \longleftrightarrow X[-k]$$

If $x[n]$ is a real-value sequence and an even function

• $x[n] = x[-n] \rightarrow X[k] = X[-k]$
  • $|X[k]| = |X[-k]|$ -> Amplitude spectrum is an even function
  • $\angle X[k] = \angle X[-k]$ -> Phase spectrum is an even function

But If $x[n]$ is a real-value sequence only, Phase spectrum is an odd function.

Since Phase spectrum is both odd and even function -> Phase spectrum = 0

Therefore If $x[n]$ is a real-value sequence and $x[n] = x[-n]$ (even function) , Phase spectrum = 0

DTFS Example

Forward DTFS

Reconstructing x[n] (Inverse DTFS)

Practice Questions

As we are given the X[k] of We will be using property to do these questions.

Key info of this question:

DTFS - x[n] is periodic

Time-shift:

$$x\left[n-n_{0}\right] \longleftrightarrow e^{-j 2 \pi k \frac{n_{0}}{N}} X[k]$$

Time-reversal:

$$x[-n] \longleftrightarrow X[-k]$$

$x[n] = [1\space1\space0\space0]$ (Given)

$X[k] = \{0.5,\space(0.25-0.25j),\space0,\space(0.25+0.25j)\}$ (Given)

(1) $x_1[n]$ = [1 1 0 0 1 1 0 0]

It is basically the same as [1 1 0 0]. Period = 4

$x_1[n] = x[n]$

$X_1[k] = X[k] = \{0.5,\space(0.25-0.25j),\space0,\space(0.25+0.25j)\}$

Note:

A sequence of period $N$ is also a sequence of period $nN$, where $n$ is a +ve integer.

If you consider it as a sequence of period $nN$ and compute the DTFS for the sequence, the output is a spectrum of period $nN$.

$$X^{\prime}[n k]=\left\{\begin{array}{cc} X[k] & \text { for integer } k \\ 0 & \text { else } \end{array}\right.$$

Now in our case, $n = 2$.

X[0] -> X[0] ,

X[1] -> X[2],

X[2] -> X[4],

X[3] -> X[6]

$X_1[k] = X[2k] = \{0.5,\space0,\space(0.25-0.25j),\space0,\space0,\space0,\space(0.25+0.25j),\space0\}$

Therefore solution for (1) is $X_1[k] = \{0.5,\space0,\space0.25-0.25j,\space0,\space0,\space0,\space0.25+0.25j,\space0\}$

(2) $x_2[n]$ = [0 1 1 0]

It is a shifted version of [1 1 0 0]. Shift to right 1 unit -> $x[n-1]$

$x_2[n] = x[n-1]$

$X_2[k] = e^{-j2\pi k\frac{1}{4}}X[k] = e^{-j\pi\frac{1}{2}k}X[k] = (-j)^kX[k]$

$(-j)^kX[k] = \{0.5\times 1,\space(0.25-0.25j)\times (-j)^1,\space0\times(-j)^2,\space(0.25+0.25j)\times(-j)^3\}$

$X_2[k] = \{0.5,\space(-0.25-0.25j),\space0,\space(-0.25+0.25j)\}$

Therefore solution for (2) is $X_2[k] = \{0.5,\space(-0.25-0.25j),\space0,\space(-0.25+0.25j)\}$

Note: Magnitude spectrum $|X_2[k]| = |X[k]|$ as $e^{j2\pi k \frac{1}{4}}$ does not affect the magnitude.

(3) $x_3[n]$ = [0 0 1 1]

Again, It is a shifted version of [1 1 0 0]. Shift to right 2 unit -> $x[n-2]$

$x_3[n] = x_2[n-1] = x[n-2]$

$X_3[k] = e^{-j2\pi k \frac{2}{4}}X[k] = e^{-j\pi k}X[k] = (-1)^kX[k]$

$(-1)^kX[k] = \{0.5\times(-1)^0,\space(0.25-0.25j)\times(-1)^1,\space0\times(-1)^2,\space(0.25+0.25j)\times(-1)^3\}$

$X_3[k] = \{0.5,\space(-0.25+0.25j),\space0,\space(-0.25-0.25j)\}$

Therefore solution for (3) is $X_3[k] = \{0.5,\space(-0.25+0.25j),\space0,\space(-0.25-0.25j)\}$

Note: Magnitude spectrum $|X_3[k]| = |X[k]|$ as $e^{j2\pi k \frac{2}{4}}$ does not affect the magnitude.

(4) $x_4[n]$ = [1 0 0 1]

Method 1

It is flipped version of $x[n]$.

Note: you need to mind which one is the $x[n]$ (We get $x[-n]$ by flipping $x[n]$ about $x[0]$)

$x_4[n] = x[-n]$

$X_4[k] = X[-k]$

$X[k] = \{0.5,\space(0.25-0.25j),\space0,\space(0.25+0.25j)\}$ (Given)

After flipped:

$X[-k] = \{0.5,\space(0.25+0.25j),\space0,\space(0.25-0.25j)\}$

Therefore solution for (4) is $X_4[k] = \{0.5,\space(0.25+0.25j),\space0,\space(0.25-0.25j)\}$

Method 2

It is a shifted version of [1 1 0 0]. Shift to left 1 unit -> $x[n+1]$

$x_4[n] = x[n+1]$

$X_4[k] = e^{-j2\pi k\frac{-1}{4}}X[k] = (\frac{-1}{j})^kX[k] = (j)^kX[k]$

$(j)^kX[k] = \{0.5\times(j)^0,\space(0.25-0.25j)\times(j)^1,\space0\times(j)^2,\space(0.25+0.25j)\times(j)^3\}$

$X_4[k] = \{0.5,\space(0.25+0.25j),\space0,\space(0.25-0.25j)\}$

Therefore solution for (4) is $X_4[k] = \{0.5,\space(0.25+0.25j),\space0,\space(0.25-0.25j)\}$

Note: Magnitude spectrum $|X_4[k]| = |X[k]|$

• $|X[k]| = |X[-k]|$ -> Amplitude spectrum is an even function

FIrst, find the period.

Period = 8 (Given)

As Amplitude Spectrum of a real-value periodic sequence is an even function.

To complete the amplitude spectrum, just make it periodic.

Note: For k = -4:4 , the range is 8 = period.

• Period determines how the amplitude spectrum look like.

Discrete-time Fourier Transform (DTFT)

Used to analyze a aperiodic discrete-time signal

Connection between DTFS and DTFT:

• $\frac{2\pi k}{N} = \Omega$
• $\Omega$ is a continuous variable, and periodic with $2\pi$

Definition

Inverse DTFT

$$X(\Omega) \longrightarrow x[n]=\frac{1}{2 \pi} \int_{-\pi}^{\pi} X(\Omega) e^{j \Omega n} d \Omega$$

Forward DTFT

$$x[n] \longrightarrow X(\Omega)=\sum_{n=-\infty}^{\infty} x[n] e^{-j \Omega n}$$

Properties

DTFT and inverse DTFT are linear. (Homogeneous + Additive) -> enable us to use shortcut to get answer

x[n] and time-shifted x[n] have same magnitude spectrum.

$x[n] \rightarrow X(\Omega) = \sum^\infty_{n=-\infty} x[n]e^{-j\Omega n}$

$x[n-n_0] \rightarrow X^{new}(\Omega) = e^{-j\Omega n_0} X(\Omega)$

DTFT is periodic with period $2\pi$.

$X(\Omega + 2\pi) = X(\Omega)$

DTFT Example

Forward DTFT

Inverse DTFT

DTFT vs DTFS

Connection between DTFS and DTFT

• $\Omega = 2\pi k/N$ is the normalized freq
• $N \rightarrow \infty \rightarrow$
  • $\Omega$ is a continuous variable
  • $\Omega$ is periodic with 2$\pi$

Basically

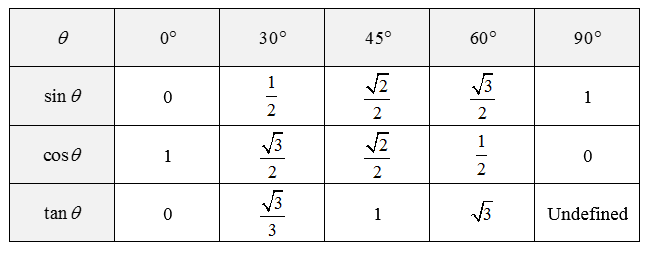
In Polar form $z = \rho e^{j\theta}$

• $\rho$ is the Amplitude
• $\theta$ is the Phase

In Retangular form $z = a+jb$

$|X[k]| = \sqrt{a^2+b^2}$ for each term

$\angle X[k] = tan^{-1}\frac{b}{a}$ for each term

• Amplitude spectrum must be even
• Phase spectrum must be odd

Periodic in one domain = Discrete in another domain

Aperiodic in one domain = Continuous in another domain

• A signal having a discrete spectrum must be periodic time signal.
• A signal having a periodic spectrum must be discrete time signal.

Euler’s Relation

$2cos\theta = e^{j \theta} + e^{-j \theta}$

$2jsin\theta = e^{j\theta} - e^{-j\theta}$

$sin(\theta) = cos(\frac{\pi}{2} - \theta) = cos(\theta - \frac{\pi}{2})$

$cos(-\alpha) = cos(\alpha) = cos(2k\pi - \alpha)$

• DTFT is for discrete time aperiodic signals to derive their amplitude and phase spectrum
  • both amplitude and phase spectrum is continuous
• DTFS is for discrete time periodic signals to derive their amplitude and phase spectrum
  • both amplitude and phase spectrum is discrete
• CTFT is for continuous time aperiodic signals to derive their amplitude and phase spectrum
  • both amplitude and phase spectrum is continuous
• CTFS is for continuous time periodic signals to derive their amplitude and phase spectrum
  • both amplitude and phase spectrum is discrete

• A continuous time signal may not be perfectly reconstructed with sufficient number of terms in its Fourier series.
• A discrete time signal can be perfectly reconstructed with sufficient number of terms in its Fourier series.

Relations Among Fourier Methods

CTFS

CTFT

DTFS

DTFT

Discrete Fourier Transform (DFT)

Note: Discrete Fourier Transform (DFT) =/= Discrete-time Fourier Transform (DTFT)

Main Concept:

• Sampling the spectrum and Keep the samples only.
• Just keeping one period of the spectrum only.

Basic Idea, DFT help you to skip steps.

DTFT route: $x[n] \rightarrow \text{DTFT} \rightarrow X(\Omega) \rightarrow Sampling\rightarrow X[k]$

DFT route: $x[n] \rightarrow \text{DFT} \rightarrow X[k]$

The Idea of DFT

Definition

It actually looks like DTFS. nearly no difference.

Forward DFT

k : marks the frequency

N : number of samples we sample a period of the spectrum

• A DFT of length N is called a N-point DFT.

$$x[n] \longrightarrow X[k]=\sum_{n=0}^{N-1} x[n] e^{-j 2 \pi \frac{k}{N} n}$$

Note: X[0] is the DC component

• $X[0]=N \bar{x}$

Inverse DFT

k : marks the frequency

N : number of samples we sample a period of the spectrum

• A DFT of length N is called a N-point DFT.

$$X[k] \longrightarrow x[n]=\frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j 2 \pi \frac{k}{N} n}$$

Relation Between DFT and DTFT

DFT Spectrum matches DTFT Spectrum exactly, but at a finite no of points only.

• DTFT: produces smooth functions of frequency,
• DFT: produces sampled versions of the same spectra

Resolution of DFT Spectrum

DFT spectrum has N points to cover a range of frequencies from 0 to 2$\pi$, each frequency separates by $2\pi/N$

Resolution = frequency spacing of DFT

The higher the value N, the better the resolution of the frequency spectrum.

Resolution Issue

Sometimes, the resolution might not be fine enough to characterize the spectrum

The spectrum resolution can be improved by increasing $N$.

Use of DFT

When we see an aperiodic discrete time signal

• We chop one of its segments (or the whole segment if its length is finite)
• repeat the segment an infinite number of times to construct a virtual periodic discrete-time signal
• Represent the virtual periodic signal with DTFS to study its spectrum.

Useful Tables

Practice Questions for DFT and DTFT

(a) $x_a[n] = 0.5^n u[n]$

Method 1

From Table, You can see this formula:

$$a^{n} u[n] \leftrightarrow \frac{1}{1-a e^{-j \Omega}},|a|<1$$

Sub $0.5$ into $a$, you get $x_a[n] = 0.5^n u[n] \leftrightarrow X_a(\Omega) = \frac{1}{1-0.5e^{-j\Omega}}$

Method 2

This is how $0.5^n u[n]$ looks like. (Not scaled to graph)

$x_a[n] = 0.5^n u[n] = \delta[n] + 0.5^1\delta[n-1] + 0.5^2\delta[n-2] +\cdots+ 0.5^k\delta[n-k] + \cdots$

Using the transform table, you will see:

$x_a[n] \leftrightarrow X_a(\Omega) = 1 + 0.5e^{-j\Omega} + 0.5^2e^{-j2\Omega} +\cdots+ 0.5^ke^{-jk\Omega} + \cdots$

According the Geometric progression formula (Geometric Sequence):

• Ratio $r = 0.5e^{-j\Omega}$
• First Term $a = 1$

Therefore $X_a(\Omega) = \frac{1}{1-0.5 e^{j\Omega}}$

(b) $x_a[n] = n \cdot0.5^n u[n]$

From Table, You can see this formula: Multiplication by $n$

$$n x[n] \leftrightarrow j \frac{d}{d \Omega} X(\Omega)$$

Basically, $x_b[n] = n\cdot x_a[n]$

Therefore $X_b(\Omega) = j\frac{d}{d\Omega}X_a(\Omega)$

Do a differentiation.

Hint : $f(x) = x^r \longrightarrow f'(x) = rx^{r-1}$

Hint: Chain Rule

Hint: $f(x) = e^{ax} \longrightarrow f'(x) = ae^{ax}$

$\frac{d}{d\Omega}X_a(\Omega) = (-1) \times (1-0.5e^{-j\Omega})^{-2}\times(0-0.5\times -je^{-j\Omega})$

$= (-1)\times(1-0.5e^{-j\Omega})^{-2}\times(0.5je^{-j\Omega})$

= $\frac{-j0.5e^{-j\Omega}}{(1-0.5e^{-j\Omega})^{2}}$

$X_b(\Omega) = j\frac{d}{d\Omega}X_a(\Omega) = j\frac{-j0.5e^{-j\Omega}}{(1-0.5e^{-j\Omega})^{2}}$

Since $j \times - j = 1$

$X_b(\Omega) = \frac{0.5e^{-j\Omega}}{(1-0.5e^{-j\Omega})^{2}}$

(a) $v[n] = x[n-5]$

From Table, you can see this formula: Time Shift

$$x[n-q] \leftrightarrow X(\Omega) e^{-j q \Omega}, q \text { is any integer }$$

$V(\Omega) = X(\Omega)\cdot e^{-j5\Omega} = \frac{e^{-j5\Omega}}{e^j\Omega + b}$

(b) $v[n] = n\cdot x[n]$

From Table, You can see this formula: Multiplication by $n$

$$n x[n] \leftrightarrow j \frac{d}{d \Omega} X(\Omega)$$

$V(\Omega) = j\frac{d}{d\Omega}X(\Omega) = j\frac{d}{d\Omega}(\frac{1}{e^{j\Omega} + b})$

Do a differentiation.

Hint : $f(x) = x^r \longrightarrow f'(x) = rx^{r-1}$

Hint: Chain Rule

Hint: $f(x) = e^{ax} \longrightarrow f'(x) = ae^{ax}$

$\frac{d}{d\Omega}(\frac{1}{e^{j\Omega} + b}) = \frac{d}{d\Omega}(e^{j\Omega}+b)^{-1} = (-1)\times (e^{j\Omega} + b)^{-2} \times (je^{\Omega}+0) = \frac{-je^{\Omega}}{(e^{j\Omega}+b)^2}$

Since $j \times - j = 1$

$V(\Omega) = j\frac{-je^{\Omega}}{(e^{j\Omega}+b)^2} = \frac{e^{j\Omega}}{(e^{j\Omega}+b)^2}$

(a) $x_{c}[n]=n \cdot 0.5^{n} \cdot \cos (4 n) \cdot u[n]$

$x_{c}[n]=n \cdot 0.5^{n}\cdot u[n] \cdot \cos (4 n)$

We break it into serval steps and store it with different variables.

Let $y[n] = (0.5)^n u[n] \leftrightarrow Y(\Omega) = \frac{1}{(1-0.5e^{-j\Omega})}$

Let $z[n] = n\cdot u[n] \leftrightarrow Z(\Omega) = j\frac{d}{d\Omega}(Y(\Omega)) = \frac{0.5e^{-j\Omega}}{(1-0.5e^{-j\Omega})^2}$

$x_c[n] = z[n]cos(4n) \leftrightarrow X_c(\Omega) = \frac{1}{2}[Z(\Omega + 4) + Z(\Omega-4)]$

$X_{c}(\Omega)=\frac{1}{2} \cdot\left\{\frac{0.5 e^{-j(\Omega+4)}}{\left(1-0.5 e^{-j(\Omega+4)}\right)^{2}}+\frac{0.5 e^{-j(\Omega-4)}}{\left(1-0.5 e^{-j(\Omega-4)}\right)^{2}}\right\}$

(b) $x_{d}[n]=(0.5)^{|n |} \quad-\infty<n<\infty$

you need to know what it is exactly.

The first graph is how $(0.5)^{|n|}$ looks like. (Not scaled to graph)

It is basically $0.5^n u[n]$ + a flipped $0.5^n u[n]$ - a overlapped pulse.

$x_{d}[n]=(0.5)^{|n |} = (0.5)^n u[n] + (0.5)^{-n} u[-n] - \delta[n]$

Break it down into serveral steps.

Let $f[n] = (0.5)^n u[n] \longleftrightarrow F(\Omega) = \frac{1}{1-0.5e^{-j\Omega}}$

$f[-n] = (0.5)^{-n} u[-n] \longleftrightarrow F(-\Omega) = \frac{1}{1-0.5e^{j\Omega}}$

Therefore

$x_d[n] = f[n] + f[-n] - \delta[n] \longleftrightarrow X_d(\Omega) = F(\Omega) + F(-\Omega) - 1$

$X_d(\Omega) = \frac{1}{1-0.5e^{-j\Omega}} + \frac{1}{1-0.5e^{j\Omega}} - 1$

Do a simplification

$X_d(\Omega) = \frac{1}{1-0.5e^{-j\Omega}} + \frac{0.5e^{j\Omega}}{1-0.5e^{j\Omega}} = \frac{1-0.5e^{-j\Omega}+0.5e^{j\Omega}-0.25}{1-0.5e^{-j\Omega}-0.5e^{j\Omega}+0.25}= \frac{0.75}{1.25-cos\Omega}$

Basically the hardest step is simplification -.-

(a) $v[n] = x[n] - x[n-1]$

$V(\Omega) = X(\Omega) + X(\Omega) e^{-j\Omega} = \frac{1}{e^{j\Omega} + b} - \frac{e^{-j\Omega}}{e^{j\Omega}+b}$

$V(\Omega) = \frac{1}{e^{j\Omega} + b}\cdot(1-e^{-j\Omega})$

(b) $v[n]=x[n] \otimes x[n]$

$V(\Omega) = X(\Omega) \times X(\Omega) = \frac{1}{(e^{\Omega-2}+b)^2}$

© $v[n] = x[n] e^{j2n}$

$V(\Omega) = X(\Omega-2) = \frac{1}{e^{\Omega-2}+b}$

(a) Obtain the 3 point DFT.

Forward DFT formula:

$$x[n] \longrightarrow X[k]=\sum_{n=0}^{N-1} x[n] e^{-j 2 \pi \frac{k}{N} n}$$

Length = $N = 3$

$X[k] = \sum^{3-1}_{n=0}x[n]e^{-j2\pi \frac{nk}{3}}$

$X[k] = 1\times e^{-j2\pi\frac{0k}{3}} + 0 \times e^{-j2\pi\frac{1k}{3}} + -1 \times e^{-j2\pi\frac{2k}{3}}$

$X[k] = 1 - e^{-j\pi k \frac{4}{3}}$

$X[0] = 1 - e^{-j\pi \frac{4\times0}{3}} = 1-1 = 0$

$X[1] = 1 - e^{-j\pi \frac{4\times1 }{3}} = 1 - (cos\frac{4\pi}{3} - jsin\frac{4\pi}{3}) = 1.5-0.8666j = 1.7321e^{-j0.5236}$

$X[2] = 1 - e^{-j\pi \frac{4\times2 }{3}} = 1 - (cos\frac{8\pi}{3} - jsin\frac{8\pi}{3}) = 1.5+0.8666j = 1.7321e^{j0.5236}$

(b) Obtain the 6 point DFT.

Forward DFT formula:

$$x[n] \longrightarrow X[k]=\sum_{n=0}^{N-1} x[n] e^{-j 2 \pi \frac{k}{N} n}$$

Length = $N = 6$

$X[k] = \sum^{6-1}_{n=0}x[n]e^{-j2\pi \frac{nk}{6}}$

$X[k] = 1\times e^{-j2\pi\frac{0k}{6}} + 0 \times e^{-j2\pi\frac{1k}{6}} + -1 \times e^{-j2\pi\frac{2k}{6}}$

$X[k] = 1 - e^{-j\pi k \frac{4}{6}} = 1-e^{-j\pi k \frac{2}{3}}$

$X[0] = 1 - e^{-j\pi \frac{2\times0}{3}} = 1-1 = 0$

$X[1] = 1 - e^{-j\pi \frac{2\times1 }{3}} = 1 - (cos\frac{2\pi}{3} - jsin\frac{2\pi}{3}) = 1.5+0.8666j = 1.7321e^{j0.5236}$

$X[2] = 1 - e^{-j\pi \frac{2\times2 }{3}} = 1 - (cos\frac{4\pi}{3} - jsin\frac{4\pi}{3}) = 1.5-0.8666j = 1.7321e^{-j0.5236}$

$X[3] = 1-e^{-j\pi\frac{2\times3}{3}} = 1 - (cos2\pi - jsin2\pi) = 0$

$X[4] = 1 - e^{-j\pi\frac{2\times4}{3}} = 1- (cos\frac{8\pi}{3}-jsin\frac{8\pi}{3}) = 1.5+0.8666j = 1.7321e^{-j0.5236}$

$X[5] = 1 - e^{-j\pi\frac{2\times5}{3}} = 1- (cos\frac{10\pi}{3}-jsin\frac{10\pi}{3}) = 1.5-0.8666j = 1.7321e^{-j0.5236}$

©

4-point DFT equation:

$$X[k]=\sum_{n=0}^{3} x[n] e^{-j 2 \pi \frac{k n}{4}}$$

(a) x[n] = [1 0 1 0]

$X[k] = 1 + 0 + 1\times e^{-j2\pi\frac{2k}{4}} + 0 = 1 + e^{-j\pi k}$

$X[0] = 1 + 1 = 2$

$X[1] = 1 + e^{-j1\pi} = 1 - 1 = 0$

$X[2] = 1 + e^{-j2\pi} = 1 + 1 = 2$

$X[3] = 1 + e^{-j3\pi} = 1 - 1 = 0$

(b) x[n] = [1 0 -1 0]

$X[k] = 1 + 0 + (-1)\times e^{-j2\pi\frac{2k}{4}} + 0 = 1 - e^{-j\pi k}$

$X[0] = 1 - 1 = 0$

$X[1] = 1 - e^{-j1\pi} = 1 + 1 = 2$

$X[2] = 1 - e^{-j2\pi} = 1 - 1 = 0$

$X[3] = 1 - e^{-j3\pi} = 1 + 1 = 2$

© x[n] = [-1 0 1 2]

$X[k] = -1 + 0 + 1\times e^{-j2\pi\frac{2k}{4}} + 2\times e^{-j2\pi\frac{3k}{4}} = -1 + e^{-j\pi k} + 2e^{-j\pi k \frac{3}{2}}$

$X[0] = -1 + 1 + 2 = 2$

$X[1] = -1 + e^{-j1\pi} + 2e^{-j\pi\frac{3\times 1}{2}} = -1 - 1 + 2j = -2 + 2j$

$X[2] = -1 + e^{-j2\pi} + 2e^{-j\pi\frac{3\times 2}{2}} = -1 + 1 + 2e^{-j3\pi} = -1 + 1 - 2 = -2$

$X[3] = -1 + e^{-j3\pi} + 2e^{-j\pi\frac{3\times 3}{2}} = -1 - 1 + 2(-j) = -2 - 2j$

Discrete-time System Analysis via the DTFT and DFT

Recall: LTI System

linear time-invariant discrete-time systems (LTI system)

system outputs for a given input can be determined via a time domain system analysis

Output = input convolve with unit-pulse response

$$y[n]=\sum_{i=0}^{M-1} h[i] x[n-i]$$

we can also determine the output via a frequency domain system analysis.

LTI system can respond to some basic input signals in frequency domain:

• Exponential input
• Cosine input
• Periodic input
• Aperiodic input

Discrete-time Signals

In frequency domain, DT signals are represented as

• Discrete time Fourier series
  • for periodic signals
• Discrete time Fourier transform or Discrete Fourier transform
  • for aperiodic signals

Frequency response (DTFT of h[n])

Tells how the system responds to individual frequency components of the input.

Basically = DTFT of $h[n]$

DTFT formula:

$$H(\Omega)=\sum_{i=-\infty}^{\infty} h[i] e^{-j \Omega i}=\sum_{i=0}^{M-1} h[i] e^{-j \Omega i}$$

Recall :

You can get impulse response $h[n]$ from the difference equation.

Then by changing the domain (Fouries Transform), you get $H(\omega)$.

Note:

$$\mathrm{ae}^{-\mathrm{jk} \omega} \leftrightarrow \mathrm{a} \delta[\mathrm{n}-\mathrm{k}]$$

Learn to get common factors from $e^{j\omega}$.

$e^{-aj\omega} + e^{-bj\omega} = e^{\frac{-a-b}{2}}(e^{\frac{|-b+a|}{2}}+e^{\frac{-|-b+a|}{2}})$

• e.g. $e^{-j\omega} + e^{-2j\omega} = e^{-1.5j\omega} (e^{0.5j\omega}+e^{-0.5j\omega})$

$(e^{a} + e^{-a}) = 2cos(a)$

LTI system responds to Exponential input

$$x[n]=A e^{j \phi} e^{j \hat{\omega} n}$$

$$y[n]=H(\hat{\omega}) A e^{j \phi} e^{j \hat{\omega} n}$$

where

$$H(\Omega)=\sum_{i=0}^{M-1} h[i] e^{-j \Omega i}$$

^Frequency response of system

You need to know $H(\Omega)$ then you will be able to find $y[n]$

For LTI system with Exponential input:

• Frequencies of both Input & Output signals are $\hat{\omega}$
  • Frequency does not changed by the system!
• Output signal is
  • the Input signal $\times$ the frequency response of H at frequency $\hat{\omega}$

Reminder

Note:

You can get frequency response from impulse response $h[n]$.

To know $H(\Omega)$'s mag and phase:

$H(\Omega) = |H(\Omega)|e^{j\angle H(\Omega)}$

mag = $|H(\Omega)|$

phase = $\angle H(\Omega)$

$$e^{j\Omega} + e^{-j\Omega} = 2cos\Omega$$

LTI system responds to Periodic input (DTFS)

In this case, x[n] is a periodic input. (cos input)

$$x[n]=A_{0}+\sum_{i=1}^{N} A_{i} \cos \left(\hat{\omega}_{i} n+\phi_{i}\right)$$

$$y[n]=A_{0} H(0)+\sum_{i=1}^{N} A_{i}\left|H\left(\hat{\omega}_{i}\right)\right| \cos \left[\hat{\omega}_{i} n+\phi_{i}+\angle H\left(\hat{\omega}_{i}\right)\right]$$

where

$$H(\Omega)=\sum_{i=0}^{M-1} h[i] e^{-j \Omega i}$$

^Frequency response of system

You need to know $H(\Omega)$ then you will be able to find $y[n]$

For LTI system with Periodic input:

• Frequencies of both Input & Output signals are $\hat{\omega}_i$
  • Frequency does not changed by the system!
• Output Amplitude scaled by the factor $|H(\hat{\omega}_i)|$
• Output Phase shifted by $\angle H(\hat{\omega}_i)$

LTI system responds to Aperiodic input (DTFT)

$$x[n]=\frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j 2 \pi \frac{k}{N} n}$$

$$y[n]=\frac{1}{N} \sum_{k=0}^{N-1}\{X[k] H[k]\} e^{j 2 \pi \frac{k}{N}(n)}$$

Note : $N$ = Length of h[n] + Length of x[n] – 1

where

$$H[k]=\sum_{n=0}^{N-1} h[n] e^{-j 2 \pi \frac{k}{N} n}$$

^Frequency response of system

You need to know $H[k]$ and $X[k]$ then you will be able to find $y[n]$.

You use the same DFT formula to get $X[k]$.

For LTI system with Periodic input:

• Identify $N$ should be Length of $h[n]$ + Length of $x[n]$ - 1
• Get the DFT of the input first ($X[k]$) with $N$ (use Zero Padding)
• Get the DFT of the impulse response ($H[k]$) with $N$ (use Zero Padding)
• Then Multiply X[k] and H[k] to get $Y[k]$
• Output = Inverse DFT of $X[k]H[k]$
• $N$ should be Length of $h[n]$ + Length of $x[n]$ - 1
  • the length of the linear convolution output of $h[n]$ and $x[n]$

or

• Get the convolution of $x[n]$ and $h[n]$ to get $y[n]$ directly

Zero Padding

Assume missing samples are zeros.

Connection between DFT and Convolution

convolution in time domain = multiplication in frequency domain

Useful info

$$1 \leftrightarrow \delta[n]$$

$$ae^{-jk\omega} \leftrightarrow a\delta[n-k]$$

$$X(\omega) \leftrightarrow ax[n-k]$$

$$\mathcal{H}(-\hat{\omega})=\mathcal{H}^{*}(\hat{\omega})$$

$$|\mathcal{H}(-\hat{\omega})|=|\mathcal{H}(\hat{\omega})|$$

$$\angle \mathcal{H}(-\hat{\omega})=-\angle \mathcal{H}(\hat{\omega})$$

$$\begin{aligned} \Re e\{\mathcal{H}(-\hat{\omega})\} &=\Re e\{\mathcal{H}(\hat{\omega})\} \\ \Im m\{\mathcal{H}(-\hat{\omega})\} &=-\Im m\{\mathcal{H}(\hat{\omega})\} \end{aligned}$$

Practice Questions - DFT and System

$$H(\Omega) = \sum_{k=-\infty}^{\infty} p_{2 \times \frac{\pi}{4}}(\Omega+2 \pi k)$$

Note:

$$H(\Omega) \leftrightarrow h[n]$$

$$\sum_{k=-\infty}^{\infty} p_{2 B}(\Omega+2 \pi k) \leftrightarrow \frac{B}{\pi} \operatorname{sinc}\left(\frac{B}{\pi} n\right)$$

(a)

To get h[n]:

$h[n] = \frac{\frac{\pi}{4}}{\pi}sinc(\frac{\frac{\pi}{4}}{\pi}n)$

$h[n] = \frac{1}{4}sinc(\frac{n}{4})$

(b)

(i)

Find $x[n] = cos(\frac{n\pi}{8})$

$x[n]$ has 1 AC component which frequency is $\frac{n\pi}{8}$

$H(\frac{n\pi}{8}) = 1$ (See the $H(\Omega)$ graph)

$y[n] = 1 \times cos(\frac{n\pi}{8} + 0)$

$= cos(\frac{n\pi}{8})$

(ii)

$x[n] = cos(\frac{3n\pi}{4}) + cos(\frac{n\pi}{16})$

$H(\frac{3n\pi}{4})= 0$ (See the $H(\Omega)$ graph)

$H(\frac{n\pi}{16}) = 1$ (See the $H(\Omega)$ graph)

$y[n] = 0 cos(\frac{3\pi n}{4} + 0) + 1cos(\frac{n\pi}{16} + 0)$

$= cos(\frac{n\pi}{16})$

Note :

$$\delta[n] \leftrightarrow 1$$

$$\delta[n-N] \leftrightarrow e^{-jN\Omega}$$

(a)

$h[n] = \delta[n] + \delta[n-1] + \delta[n-2] + \delta[n-3]$

$H(\Omega) = 1+e^{-j1\Omega} + e^{-j2\Omega} + e^{-j3\Omega}$

$= e^{-j0\Omega}+e^{-j1\Omega} + e^{-j2\Omega} + e^{-j3\Omega}$

$= e^{-j\Omega}(e^{j\Omega}+e^{-j\Omega}) + e^{-j2\Omega}(e^{j\Omega}+e^{-j\Omega})$

…

$= 4cos(\Omega)cos(\frac{\Omega}{2})e^{\frac{-3j\Omega}{2}}$

(b)

$x[n] = 4 + 3cos(0.2n\pi + \pi/3)$

$x[n]$ has a DC component and a AC component which frequency is $0.2n\pi$

$H(0)=4$

$H(0.2\pi) = 3.077e^{\frac{-3j0.2\pi}{2}} = 3.077e^{-0.3j\pi}$

$y[n] = 4\times 4 + 3.077\times 3cos(0.2\pi n + \frac{\pi}{3}-0.3\pi)$

$= 16 + 9.233cos(0.2\pi n+\frac{\pi}{3}-0.3\pi)$

(a)

Fastest way: Factorize and do time-domain convolution

$H(\omega)=\left(1+e^{-j \omega}\right)\left(1-e^{j \pi / 4} e^{-j \omega}\right)\left(1-e^{-j \pi / 4} e^{-j \omega}\right)$

$= (1+e^{-j\omega})(1-2cos(\frac{\omega}{4})e^{-j\omega}+e^{-2j\omega})$

Now hop to

$h[n] = \{1,1\} \otimes \{1 ,-\sqrt2,1\}$

$h[n] = \{1,(1-\sqrt2),(1-\sqrt2),1\}$

$h[n] = \delta[n] + (1-\sqrt2)\delta[n-1] + (1-\sqrt2)\delta[n-2] + \delta[n-3]$