Signal and System Analysis [2] - Fourier Series/ Transform

Fourier Series (FS)

For periodic signal.

Signals can be constructed by summing sinusoids of different frequencies, amplitudes and phases.

Signals = $A_{0}+A_{1}cos(2\pi f_{1}t + \theta_{1})+A_{2}cos(2\pi f_{2}t + \theta_{2})+A_{3}cos(2\pi f_{3}t + \theta_{3})+...$

Periodic signals can be constructed by summing sinusoids that are harmonically related (Fouries Series).

Signals = $A_{0}+A_{1}cos(2\pi f_{1}t + \theta_{1})+A_{2}cos(2\pi f_{2}t + \theta_{2})+A_{3}cos(2\pi f_{3}t + \theta_{3})+...$

Where $f_{2}=2f_{1},f_{3}=3f_{1},f_{4}=4f_{1},f_{5}=5f_{1}$

What is Fourier Series?

definition

It is a way to find out the mathematical representation of the periodic signals.

Periodic waveform = sum of sinusoids that are harmonically related

Harmonically related sinusoids: Sinusoids with frequencies that are integer multiples of a basic (fundamental) frequency

• $f_k = kf_0$

materials support

---

Fourier Series Expansion

definition

$$x(t) = \sum_{k=-\infty}^{\infty}C_{k}e^{j(2\pi k_{0}ft)}$$

$$or$$

$$x(t) = \sum_{k=-\infty}^{\infty}C_{k}e^{j\frac{2\pi k_{0}t}{T}}$$

where

$$C_{k} = \frac{1}{T_{0}}\int_{T_{0}}^{0}x(t)e^{-j2\pi \frac{kt}{T_{0}}}dt$$

Find Fourier Series Coefficient

how to do

Steps:

1. Find Frequency (Periodic signal, $f$) and Period ($T$) of $x(t)$

2. $C_{k} = f\int_{\frac{-T}{2}}^{\frac{T}{2}}x(t)e^{-j2\pi \frac{kt}{T_{0}}}dt$

3. Consider k on both terms

4. One should be $\int_{\frac{-T}{2}}^{\frac{T}{2}}1dt$ , while another is 0 because of $sin(\pi)$ (Use Euler’s Relation!)

5. Draw the Magnitude and phase spectrum of $x(t)$

Note: $\int e^{at}dt = \frac{1}{a}e^{at}$

examples

Steps :

1. Find Frequency (Periodic signal, $f$) and Period ($T$) of $x(t)$

$sin 3\pi t = sin(2\pi\cdot \frac{3}{2}t)$

Since the Period is $\frac{1}{f}$ ,

$T_1 = \frac{2}{3}$

$2cos(5\pi + 0.25\pi) = 2cos(2\pi \cdot \frac{5}{2}t + 0.25\pi)$

Since the Period is $\frac{1}{f}$ ,

$T_2 = \frac{2}{5}$

Period of $sin 3\pi t + 2cos(5\pi + 0.25\pi)$ :

LCM of $T_1$ and $T_2$ = 2

2. $C_{k} = f\int_{\frac{-T}{2}}^{\frac{T}{2}}x(t)e^{-j2\pi \frac{kt}{T_{0}}}dt$

$C_{k} = \frac{1}{2}\int_{-1}^{1}x(t)e^{-j\pi kt}dt$

$= \frac{1}{2}\int_{-1}^{1}([sin(3\pi t) + 2cos(5\pi t + 0.25\pi)]e^{-j\pi kt})dt$

3. Apply Euler’s Formula on both terms

Term 1:

$sin(3\pi t)$

$= \frac{1}{2j}(e^{j3\pi t}-e^{-j3\pi t})$

Term 2:

$2cos(5\pi t + 0.25 \pi)$

$= \frac{1}{2}(e^{j(5\pi t+0.25\pi)}+e^{-j(5\pi t+0.25\pi)})$

$= \frac{1}{2}(e^{j5\pi t}\cdot e^{j0.25\pi}+e^{-j5\pi t}+e^{-j0.25\pi})$

4. If the term is a sin function, muiltply $\frac{j}{j}$

$sin(3\pi t) = \frac{1}{2j}(e^{j3\pi t}-e^{-j3\pi t})\cdot\frac{j}{j}$

$= \frac{-j}{2}(e^{j3\pi t}-e^{-j3\pi t})$

5. For sin term, draw a factor of $-1$ to make $-$ become $+$

Since $-1 = e^{j\pi}$

$sin(3\pi t) = \frac{1}{2j}(e^{j3\pi t}-e^{-j3\pi t})\cdot\frac{j}{j}= \frac{-j}{2}(e^{j3\pi t}-e^{-j3\pi t})$

$= \frac{-j}{2}(e^{j3\pi t}+(-1)\cdot e^{-j3\pi t}) = \frac{-j}{2}(e^{j3\pi t}+e^{j\pi}\cdot e^{-j3\pi t})$

Since $-j = e^{-j0.5\pi}$

$\frac{-j}{2}(e^{j3\pi t}+e^{j\pi}\cdot e^{-j3\pi t})$

$= \frac{1}{2}e^{-j0.5\pi}(e^{j3\pi t}+e^{j\pi}\cdot e^{-j3\pi t})$

= $\frac{1}{2}(e^{-j0.5\pi}\cdot e^{j3\pi t}+e^{-j0.5\pi}\cdot e^{j\pi}\cdot e^{-j3\pi t})$

6. Now you have the polar form of 2 terms. Find the magnitude and the phase.

$2(a)$

Period is 3.

$2(b)$

Note $x(t) = \sum_{k=-\infty}^{\infty}C_{k}e^{j(2\pi k_{0}t)}$ where $C_{k} = \frac{1}{T_{0}}\int_{T_{0}}^{0}x(t)e^{-j2\pi \frac{kt}{T_{0}}}dt$

Therefore

$C_{k} = \frac{1}{T_{0}}[\int_{0}^{2}2e^{-j2\pi \frac{kt}{T_{0}}}dt + \int_{2}^{3}(-1)e^{-j2\pi \frac{kt}{T_{0}}}dt]$

A is 2, B is -1.

$2(c)$

since $k = 0$

$C_{0} = \frac{1}{T_{0}}[\int_{0}^{2}2e^{0}dt + \int_{2}^{3}(-1)e^{0}dt]$

$= \frac{1}{3}[\int_{0}^{2}2dt + \int_{2}^{3}(-1)dt] = \frac{1}{3}[(2\cdot2-2\cdot 0) +((-1)\cdot 3 - (-1)\cdot 2 )]$

$= \frac{1}{3}(4+(-1)) = 1$

$2(d)$

$C_{k} = \frac{1}{3}[\int_{0}^{2}2e^{-j2\pi \frac{kt}{T_{0}}}dt + \int_{2}^{3}(-1)e^{-j2\pi \frac{kt}{T_{0}}}dt]$

$= \frac{2}{3}(\int_{0}^{2}e^{-j\frac{2}{3}\pi kt} dt) - \frac{1}{3}(\int_{2}^{3}e^{-j\frac{2}{3}\pi kt}dt)$

Note $\int e^{at}dt = \frac{1}{a}e^{at}$

On one side:

$\frac{2}{3}\int_{0}^{2}e^{-j\frac{2}{3}\pi kt} dt$

$= \frac{2}{3}(\frac{1}{-j\frac{2}{3}\pi k})[e^{-j\frac{2}{3}\pi kt}]^2_0$

$= \frac{1}{-j\pi k}[e^{\frac{2}{3}\pi kt}]^2_0$ Now you found D is $\frac{1}{-j\pi k}$

$= \frac{1}{-j\pi k}[e^{\frac{2}{3}\pi k2}- e^{\frac{2}{3}\pi k0}]$

$= \frac{1}{-j\pi k}[e^{\frac{4}{3}\pi k}- 1]$

On the other side:

$\frac{1}{3}(\int_{2}^{3}e^{-j\frac{2}{3}\pi kt}dt)$

$= \frac{1}{3}(\frac{1}{-j\frac{2}{3}\pi kt})[e^{-j\frac{2}{3}\pi kt}]^3_2$

$= \frac{1}{-j2\pi k}[e^{-j\frac{2}{3}\pi kt}]^3_2$ Now you found E is $\frac{1}{-j2\pi k}$

$= \frac{1}{-j2\pi k} [e^{-j\frac{2}{3}\pi k3}- e^{-j\frac{2}{3}\pi k2}]$

$= \frac{1}{-j2\pi k} [e^{-j2\pi k}- e^{-j\frac{4}{3}\pi k}]$

Therefore:

$= \frac{1}{-j\pi k}[e^{\frac{4}{3}\pi k}- 1] - \frac{1}{-j2\pi k} [e^{-j2\pi k}- e^{-j\frac{4}{3}\pi k}]$

$2(e)$

Sub a 2 to make a common factor.

$= \frac{1}{-j2\pi k}2[e^{\frac{4}{3}\pi k}- 1] - \frac{1}{-j2\pi k} [e^{-j2\pi k}- e^{-j\frac{4}{3}\pi k}]$

$= \frac{1}{-j2\pi k}[2e^{\frac{4}{3}\pi k}- 2] + \frac{1}{j2\pi k} [e^{-j2\pi k}- e^{-j\frac{4}{3}\pi k}]$

$= \frac{1}{j2\pi k}(e^{-j2\pi k} - e^{-j\frac{4}{3}\pi k} - 2e^{\frac{4}{3}\pi k} + 2)$

$= \frac{1}{j2\pi k}(e^{-j2\pi k} - 3e^{-j\frac{4}{3}\pi k} + 2)$

Note $e^{-j2\pi} = 1$

$= \frac{3}{j2\pi k}(1 - 1e^{-j\frac{4}{3}\pi k})$

Make 1 to be $e^0$

$= \frac{3}{j2\pi k}(e^0 - e^{-j\frac{4}{3}\pi k})$

$= \frac{3}{j2\pi k}(e^{j\frac{2\pi k}{3}}e^{-j\frac{2\pi k}{3}} - e^{-j\frac{2}{3}2\pi k})$

Draw $e^{-j\frac{2\pi k}{3}}$

$= \frac{3}{j2\pi k}e^{-j\frac{2\pi k}{3}}(e^{j\frac{2\pi k}{3}} - e^{-j\frac{2\pi k}{3}})$

$= \frac{3}{2\pi k}e^{-j\frac{2\pi k}{3}}\frac{(e^{j\frac{2\pi k}{3}} - e^{-j\frac{2\pi k}{3}})}{j}$

Use Euler’s Formula : $sin\theta = \cfrac{e^{j\theta}-e^{-j\theta}}{2j}$

$= \frac{3}{\pi k}e^{-j\frac{2\pi k}{3}}\frac{(e^{j\frac{2\pi k}{3}} - e^{-j\frac{2\pi k}{3}})}{2j}$

$= \frac{3}{\pi k}e^{-j\frac{2\pi k}{3}} sin(\frac{2\pi k}{3})$

G is $\frac{3}{\pi k}$ and F is $\frac{2\pi k}{3}$

$2(f)$

$C_k = \frac{3}{\pi k}e^{-j\frac{2\pi k}{3}} sin(\frac{2\pi k}{3})$

$C_1 = \frac{3}{\pi}e^{-j\frac{2\pi}{3}}sin(\frac{2\pi}{3})$

$= \frac{3}{\pi}sin(\frac{2\pi}{3})e^{-j\frac{2\pi}{3}}$

$H = \frac{3}{\pi}sin(\frac{2\pi}{3}) = \frac{3\sqrt3}{4\pi}$

$\theta = \frac{2\pi}{3}$

Magnitude and Phase Spectrum

Magnitude Spectrum

Note it must be even function. (Symmetric)

y axis :

$$\left |C_k\right | = \frac{1}{2}A$$

Note: In Polar form,

$z = \rho e^{-j\theta}$

where $\rho$ is the y axis of Magnitude spectrum.

In Rectangular form $z = a + jb$,

$\left |C_k\right | = \sqrt{a^2+b^2}$

Phase Spectrum

Note it must be odd function. (Anti-symmetric)

y axis :

$$\angle C_k = tan^{-1}\frac{imaginary}{real}$$

Note: In Polar form,

$z = \rho e^{-j\theta}$

where $\theta$ is the y axis of phase spectrum.

In Rectangular form $z = a + jb$,

$\angle C_k = tan^{-1}\frac{b}{a}$

materials support

---

Fourier Transform (FT)

For non-periodic signal (No period)

Describe a continuous-time, aperiodic signal in in terms of frequency content.

The frequency components are defined for all real values of the frequency.

What is Fourier Transform?

Definition

• Fourier transform: aperiodic signal, $T\rightarrow \infty$

When T is increased,

the density of the frequency components increases

the envelope of the magnitude of the scaled spectral components remains the same.

$T\rightarrow \infty$, converge into a continuous spectrum

$$c_kT = \frac{2}{k\omega_0}sin\frac{k\omega_0}{2}=\frac{sin\frac{k\omega_0}{2}}{\frac{k\omega_0}{2}}=sinc\frac{k\omega_0}{2\pi}$$

$$\lim_{T \rightarrow \infty} c_kT = sinc\frac{\omega}{2\pi}$$

$$sinc\lambda = \frac{sin\pi\lambda}{\pi\lambda}$$

$$sinc 0 = 1$$

Fourier transform - Definition:

When carry out Fourier Transform, the Time domain changes from Time $t$ to Frequency $\omega$ or changes from Frequency $\omega$ to Time $t$.

Forward transform, i.e., time to frequency:

$$X(\omega) = \int_{-\infty }^{\infty }x(t)e^{-j\omega t} dt$$

Inverse transform, i.e., frequency to time:

$$x(t) = \frac{1}{2\pi}\int_{-\infty }^{\infty }X(\omega)e^{j\omega t}d\omega$$

The function is basically the same with Fourier Series but T become a variable.

The transform pair notation:

$$x(t) \leftrightarrow X(\omega)$$

Look at the Fourier Transform Table. (bottom)

Note $\omega = 2\pi f = 2\pi \frac{1}{T}$

Functions that you need to know

Retangular pulse

Delta Pulse Function

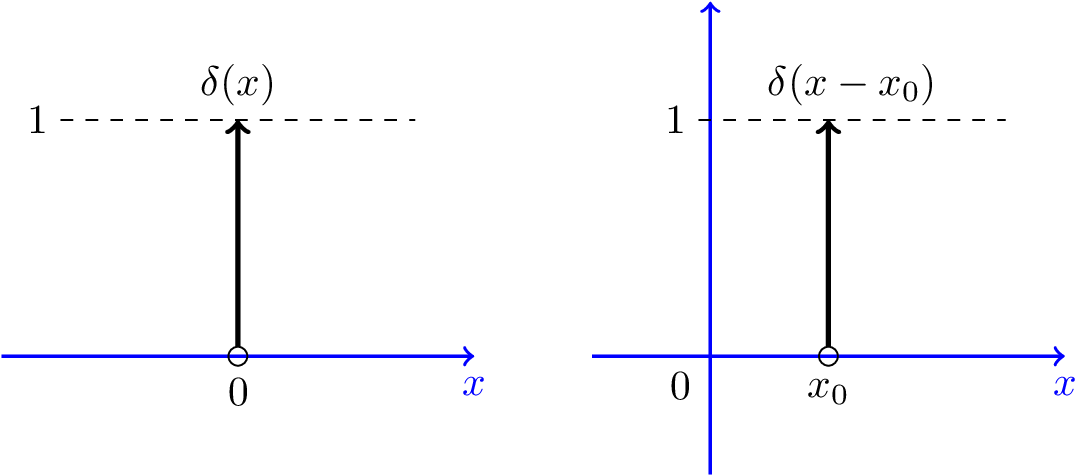
Pulse Function / Rectangular Function

$$p_{\tau}(t)$$

Exponential function

Exponential signal:

$$x(t)=\mathrm{e}^{-b t} u(t)$$

• Time-domain representation
• If b>0, exp(-bt) -> 0

What is u(t)? - Unit Step Function

The Unit Step Function - u(t)

Materials support

More about The Laplace Transform

Fourier Transform Properties

FT Properties

FT duality

Difference between FS and FT

Fourier Transform Table

---

## How to use the FT table?

examples

$(a)$

Note the formula $e^{-bt}u(t) \leftrightarrow \frac{1}{j\omega + b}$ from the table.

In this case, obviously, $b = 5$.

$x(t) = 2e^{-5t}u(t) \leftrightarrow X(\omega) = 2\cdot \frac{1}{j\omega + 5} = \frac{2}{j\omega + 5}$

$(b)$

Note the property time scaling. The formula is $x(at) \leftrightarrow \frac{1}{a}X(\frac{\omega}{a})$

$v_1(t) = x(2t) = 2e^{-5t\cdot 2}u(2t) \leftrightarrow V_1(\omega) = \frac{1}{2}X(\frac{\omega}{2}) = \frac{1}{2}\cdot \frac{2}{j\frac{\omega}{2}+5} = \frac{2}{j\omega+10}$

$(c)$

Note the property of both time scaling and time shift,

The formula is $x(at) \leftrightarrow \frac{1}{a}X(\frac{\omega}{a})$ and $x(t-c) \leftrightarrow X(\omega)e^{-j\omega c}$

$v_2(t) = x(2t-1) = x(2(t-\frac{1}{2})) \leftrightarrow V_2(\omega) = \frac{1}{2}X(\frac{\omega}{2})e^{\frac{-j\omega}{2}} = \frac{2e^{\frac{-j\omega}{2}}}{j\omega+10}$

$(d)$

$v_3(t) = 2e^{(-5+j)t}u(t) = 2e^{-5t}u(t)\cdot e^{jt} = x(t)e^{jt}$

Note the property is mulitplication by a complex exponential. The formula is $x(t)e^{j\omega_0 t} \leftrightarrow X(\omega-\omega_0)$

Therefore obviously $\omega_0 = 1$.

$v_3(t)= x(t)e^{jt} \leftrightarrow V_3(\omega) = X(\omega - \omega_0) = \frac{2}{j(\omega-1)+5}$

Questions of p(t)​

$(a)$

$Period (T) = 4 - 0 = 4$

$\tau = 4$

$x(t) = 2\cdot p_4(t-2)$

$(b)$

Note the formula : $p_\tau(t) \leftrightarrow \tau sinc\frac{\tau\omega}{2\pi}$

$x(t) = 2\cdot p_4(t-2) \leftrightarrow X(\omega) = 2\cdot 4sinc\frac{4\omega}{2\pi} = 8sinc\frac{2\omega}{\pi}$

$(c)$

$y(t) = x(t) + (- x(-t)) = x(t)-x(-t)$

$(d)$

$y(t) = x(t) - x(-t) \leftrightarrow Y(\omega) = X(\omega) - X(-\omega)$

Some Tricky Question

Let’s say you have this question.

It is obvious, this function contains time shift and can be transformed into $p_\tau (t)$ using the common form pairs.

Step 1: Check the available functions

Notice there is a $e^{-3j\omega}$.

$x(t-c) \leftrightarrow X(\omega)e^{j\omega c}$

Notice there is a $sin$ function.

$sinc\lambda = \frac{sin\pi\lambda}{\pi\lambda}$

$p_\tau(t) \leftrightarrow \tau sinc \frac{\tau\omega}{2\pi}$

Step 2: Divide the parts

$X(\omega) = \frac{4sin(3\omega)e^{-3j\omega}}{\omega} = 4 \frac{sin(3\omega)}{\omega} \cdot e^{-3j\omega}$

Step 3: Find the $\lambda$ variable

If you look closely, the formula $sinc\lambda = \frac{sin\pi\lambda}{\pi\lambda}$ requires a $\pi$.

Therefore, plug a $\frac{\pi}{\pi}$ inside.

$X(\omega) = 4 \frac{sin(3\omega)}{\omega} \cdot e^{-3j\omega} = 4\frac{sin(3\omega\frac{\pi}{\pi})}{\omega}\cdot e^{-3j\omega} = 4\frac{sin(\pi\frac{3\omega}{\pi})}{\omega}\cdot e^{-3j\omega}$

the $\lambda = \frac{3\omega}{\pi}$.

Step 4: Turn it to $sinc\lambda$

To make the bottom part match the formula $sinc\lambda = \frac{sin\pi\lambda}{\pi\lambda}$, plug another $\frac{\pi}{\pi}$.

$X(\omega)= 4\frac{sin(\pi\frac{3\omega}{\pi})}{\omega}\cdot e^{-3j\omega} = 4\frac{sin(\pi\frac{3\omega}{\pi})}{\omega}\cdot\frac{3\frac{\pi}{\pi}}{3\frac{\pi}{\pi}}\cdot e^{-3j\omega}$

$X(\omega) = 4\cdot 3\frac{\pi}{\pi}\cdot \frac{sin(\pi\frac{3\omega}{\pi})}{\omega \cdot 3\frac{\pi}{\pi}}\cdot e^{-3j\omega} = 4\cdot 3\frac{\pi}{\pi}\cdot \frac{sin(\pi\frac{3\omega}{\pi})}{\pi \cdot \frac{3\omega}{\pi}}\cdot e^{-3j\omega}$

Now you have the term $\frac{sin\pi\lambda}{\pi\lambda}$. Make it $sinc\lambda$ .

$X(\omega) = 12 \cdot sinc\frac{3\omega}{\pi}\cdot e^{-3j\omega}$

Step 5: Find the $\tau$ variable

To carry Fourier transform $p_\tau(t) \leftrightarrow \tau sinc \frac{\tau\omega}{2\pi}$, you need to make $\pi$ become $2\pi$.

$X(\omega) = 12 \cdot sinc\frac{6\omega}{2\pi}\cdot e^{-3j\omega}$

Now you get the variable $\tau$. $\tau = 6$.

$X(\omega) = 2 \cdot 6sinc\frac{6\omega}{2\pi}\cdot e^{-3j\omega}$

Step 6: Carry Fourier transform

$X(t) = 2\cdot p_6(t-3) \leftrightarrow X(\omega) = 2 \cdot 6sinc\frac{6\omega}{2\pi}\cdot e^{-3j\omega}$