Keyword/Relationship Explained
For periodic signal, Signals can be constructed by summing sinusoids of different frequencies, amplitudes and phases.
Signals = A0+A1cos(2πf1t+θ1)+A2cos(2πf2t+θ2)+A3cos(2πf3t+θ3)+...

Waveform : a plot of a function of time
Spectrum : a plot of a function of frequency
Amplitude spectrum is even, while phase spectrum is odd.
Frequency-domain representation: Represented with the set of scaling factors + phase angles.
Frequency domain analysis = get the scaling factors and the phase angles (Ai and θi )
We use different approaches for different signals.
| Signal |
Approach |
| Periodic continuous time signal |
Continuous time Fourier Series (CTFS) |
| Aperiodic continuous time signal |
Continuous time Fourier Transform (CTFT) |
| Periodic discrete time signal |
Discrete time Fourier series (DTFS) |
| Aperiodic discrete time signal |
Discrete time Fourier Transform (DTFT) |
For continuous time signal, refer to here
Discrete-time Fourier Series (DTFS)
Used to analyze a periodic discrete-time signal
- Discrete time, discrete frequency
- Periodic in time, periodic in frequency
Definition
Inverse DTFS (for getting the x[n])
x[n]: periodic, n ={0, 1, …, N-1} is time index
N is period of the input signal.
X[k]⟶x[n]=k=0∑N−1X[k]ej2πNkn
Forward DTFS (for getting the X[k])
X[k]: periodic, k={0, 1, …, N-1} is frequency index
N is period of the input signal.
x[n]⟶X[k]=N1n=0∑N−1x[n]e−j2πNkn
Properties of DTFS
Time shifting
A shift doesn’t affect the amplitude spectrum but the phase spectrum.
x[n−n0]⟷e−j2πkNn0X[k]
Frequency Shifting (Harmonic Number Shifting)
ej2πk0Nnx[n]⟷X[k−k0]
Conjugation
x∗[n]⟷X∗[−k]
If x[n] is a real-value sequence
- x[n]=x∗[n]→X[k]=X∗[−k]
- ∣X[k]∣=∣X∗[−k]∣=∣X[−k]∣ -> Amplitude spectrum is an even function
- ∠X[k]=∠X∗[−k]=−∠X[−k] -> Phase spectrum is an odd function
Time Reversal
x[−n]⟷X[−k]
If x[n] is a real-value sequence and an even function
- x[n]=x[−n]→X[k]=X[−k]
- ∣X[k]∣=∣X[−k]∣ -> Amplitude spectrum is an even function
- ∠X[k]=∠X[−k] -> Phase spectrum is an even function
But If x[n] is a real-value sequence only, Phase spectrum is an odd function.
Since Phase spectrum is both odd and even function -> Phase spectrum = 0
Therefore If x[n] is a real-value sequence and x[n]=x[−n] (even function) , Phase spectrum = 0
DTFS Example
Forward DTFS



Reconstructing x[n] (Inverse DTFS)



Practice Questions

As we are given the X[k] of We will be using property to do these questions.
Key info of this question:
DTFS - x[n] is periodic
Time-shift:
x[n−n0]⟷e−j2πkNn0X[k]
Time-reversal:
x[−n]⟷X[−k]
x[n]=[1 1 0 0] (Given)
X[k]={0.5, (0.25−0.25j), 0, (0.25+0.25j)} (Given)
(1) x1[n] = [1 1 0 0 1 1 0 0]
It is basically the same as [1 1 0 0]. Period = 4
x1[n]=x[n]
X1[k]=X[k]={0.5, (0.25−0.25j), 0, (0.25+0.25j)}
Note:
A sequence of period N is also a sequence of period nN, where n is a +ve integer.
If you consider it as a sequence of period nN and compute the DTFS for the sequence, the output is a spectrum of period nN.
X′[nk]={X[k]0 for integer k else
Now in our case, n=2.
X[0] -> X[0] ,
X[1] -> X[2],
X[2] -> X[4],
X[3] -> X[6]
X1[k]=X[2k]={0.5, 0, (0.25−0.25j), 0, 0, 0, (0.25+0.25j), 0}
Therefore solution for (1) is X1[k]={0.5, 0, 0.25−0.25j, 0, 0, 0, 0.25+0.25j, 0}
(2) x2[n] = [0 1 1 0]
It is a shifted version of [1 1 0 0]. Shift to right 1 unit -> x[n−1]
x2[n]=x[n−1]
X2[k]=e−j2πk41X[k]=e−jπ21kX[k]=(−j)kX[k]
(−j)kX[k]={0.5×1, (0.25−0.25j)×(−j)1, 0×(−j)2, (0.25+0.25j)×(−j)3}
X2[k]={0.5, (−0.25−0.25j), 0, (−0.25+0.25j)}
Therefore solution for (2) is X2[k]={0.5, (−0.25−0.25j), 0, (−0.25+0.25j)}
Note: Magnitude spectrum ∣X2[k]∣=∣X[k]∣ as ej2πk41 does not affect the magnitude.
(3) x3[n] = [0 0 1 1]
Again, It is a shifted version of [1 1 0 0]. Shift to right 2 unit -> x[n−2]
x3[n]=x2[n−1]=x[n−2]
X3[k]=e−j2πk42X[k]=e−jπkX[k]=(−1)kX[k]
(−1)kX[k]={0.5×(−1)0, (0.25−0.25j)×(−1)1, 0×(−1)2, (0.25+0.25j)×(−1)3}
X3[k]={0.5, (−0.25+0.25j), 0, (−0.25−0.25j)}
Therefore solution for (3) is X3[k]={0.5, (−0.25+0.25j), 0, (−0.25−0.25j)}
Note: Magnitude spectrum ∣X3[k]∣=∣X[k]∣ as ej2πk42 does not affect the magnitude.
(4) x4[n] = [1 0 0 1]
Method 1
It is flipped version of x[n].
Note: you need to mind which one is the x[n] (We get x[−n] by flipping x[n] about x[0])

x4[n]=x[−n]
X4[k]=X[−k]
X[k]={0.5, (0.25−0.25j), 0, (0.25+0.25j)} (Given)
After flipped:

X[−k]={0.5, (0.25+0.25j), 0, (0.25−0.25j)}
Therefore solution for (4) is X4[k]={0.5, (0.25+0.25j), 0, (0.25−0.25j)}
Method 2
It is a shifted version of [1 1 0 0]. Shift to left 1 unit -> x[n+1]
x4[n]=x[n+1]
X4[k]=e−j2πk4−1X[k]=(j−1)kX[k]=(j)kX[k]
(j)kX[k]={0.5×(j)0, (0.25−0.25j)×(j)1, 0×(j)2, (0.25+0.25j)×(j)3}
X4[k]={0.5, (0.25+0.25j), 0, (0.25−0.25j)}
Therefore solution for (4) is X4[k]={0.5, (0.25+0.25j), 0, (0.25−0.25j)}
Note: Magnitude spectrum ∣X4[k]∣=∣X[k]∣
- ∣X[k]∣=∣X[−k]∣ -> Amplitude spectrum is an even function

FIrst, find the period.
Period = 8 (Given)
As Amplitude Spectrum of a real-value periodic sequence is an even function.

To complete the amplitude spectrum, just make it periodic.
Note: For k = -4:4 , the range is 8 = period.
- Period determines how the amplitude spectrum look like.

Discrete-time Fourier Transform (DTFT)
Used to analyze a aperiodic discrete-time signal
Connection between DTFS and DTFT:
- N2πk=Ω
- Ω is a continuous variable, and periodic with 2π
Definition
Inverse DTFT
X(Ω)⟶x[n]=2π1∫−ππX(Ω)ejΩndΩ
Forward DTFT
x[n]⟶X(Ω)=n=−∞∑∞x[n]e−jΩn
Properties
DTFT and inverse DTFT are linear. (Homogeneous + Additive) -> enable us to use shortcut to get answer
x[n] and time-shifted x[n] have same magnitude spectrum.
x[n]→X(Ω)=∑n=−∞∞x[n]e−jΩn
x[n−n0]→Xnew(Ω)=e−jΩn0X(Ω)
DTFT is periodic with period 2π.
X(Ω+2π)=X(Ω)
DTFT Example
Forward DTFT


Inverse DTFT


DTFT vs DTFS

Connection between DTFS and DTFT
- Ω=2πk/N is the normalized freq
- N→∞→
- Ω is a continuous variable
- Ω is periodic with 2π
Basically
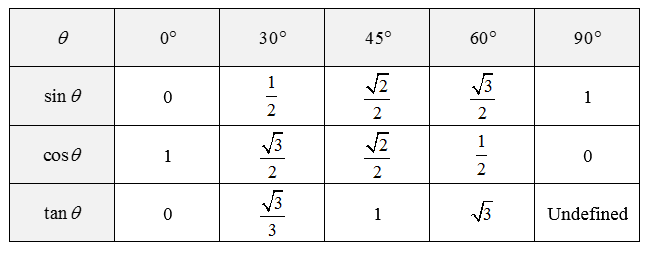
In Polar form z=ρejθ
- ρ is the Amplitude
- θ is the Phase
In Retangular form z=a+jb
∣X[k]∣=a2+b2 for each term
∠X[k]=tan−1ab for each term

- Amplitude spectrum must be even
- Phase spectrum must be odd
Periodic in one domain = Discrete in another domain
Aperiodic in one domain = Continuous in another domain
- A signal having a discrete spectrum must be periodic time signal.
- A signal having a periodic spectrum must be discrete time signal.
Euler’s Relation
2cosθ=ejθ+e−jθ
2jsinθ=ejθ−e−jθ


sin(θ)=cos(2π−θ)=cos(θ−2π)
cos(−α)=cos(α)=cos(2kπ−α)
- DTFT is for discrete time aperiodic signals to derive their amplitude and phase spectrum
- both amplitude and phase spectrum is continuous
- DTFS is for discrete time periodic signals to derive their amplitude and phase spectrum
- both amplitude and phase spectrum is discrete
- CTFT is for continuous time aperiodic signals to derive their amplitude and phase spectrum
- both amplitude and phase spectrum is continuous
- CTFS is for continuous time periodic signals to derive their amplitude and phase spectrum
- both amplitude and phase spectrum is discrete
- A continuous time signal may not be perfectly reconstructed with sufficient number of terms in its Fourier series.
- A discrete time signal can be perfectly reconstructed with sufficient number of terms in its Fourier series.
Relations Among Fourier Methods
CTFS

CTFT

DTFS

DTFT

Discrete Fourier Transform (DFT)
Note: Discrete Fourier Transform (DFT) =/= Discrete-time Fourier Transform (DTFT)
Main Concept:
- Sampling the spectrum and Keep the samples only.
- Just keeping one period of the spectrum only.
Basic Idea, DFT help you to skip steps.
DTFT route: x[n]→DTFT→X(Ω)→Sampling→X[k]
DFT route: x[n]→DFT→X[k]
The Idea of DFT

Definition
It actually looks like DTFS. nearly no difference.
Forward DFT
k : marks the frequency
N : number of samples we sample a period of the spectrum
- A DFT of length N is called a N-point DFT.
x[n]⟶X[k]=n=0∑N−1x[n]e−j2πNkn
Note: X[0] is the DC component
- X[0]=Nxˉ
Inverse DFT
k : marks the frequency
N : number of samples we sample a period of the spectrum
- A DFT of length N is called a N-point DFT.
X[k]⟶x[n]=N1k=0∑N−1X[k]ej2πNkn
Relation Between DFT and DTFT
DFT Spectrum matches DTFT Spectrum exactly, but at a finite no of points only.
- DTFT: produces smooth functions of frequency,
- DFT: produces sampled versions of the same spectra
Resolution of DFT Spectrum
DFT spectrum has N points to cover a range of frequencies from 0 to 2π, each frequency separates by 2π/N
Resolution = frequency spacing of DFT
The higher the value N, the better the resolution of the frequency spectrum.
Resolution Issue
Sometimes, the resolution might not be fine enough to characterize the spectrum
The spectrum resolution can be improved by increasing N.
Use of DFT
When we see an aperiodic discrete time signal
- We chop one of its segments (or the whole segment if its length is finite)
- repeat the segment an infinite number of times to construct a virtual periodic discrete-time signal
- Represent the virtual periodic signal with DTFS to study its spectrum.

Useful Tables



Practice Questions for DFT and DTFT

(a) xa[n]=0.5nu[n]
Method 1
From Table, You can see this formula:
anu[n]↔1−ae−jΩ1,∣a∣<1
Sub 0.5 into a, you get xa[n]=0.5nu[n]↔Xa(Ω)=1−0.5e−jΩ1
Method 2

This is how 0.5nu[n] looks like. (Not scaled to graph)
xa[n]=0.5nu[n]=δ[n]+0.51δ[n−1]+0.52δ[n−2]+⋯+0.5kδ[n−k]+⋯
Using the transform table, you will see:
xa[n]↔Xa(Ω)=1+0.5e−jΩ+0.52e−j2Ω+⋯+0.5ke−jkΩ+⋯
According the Geometric progression formula (Geometric Sequence):

- Ratio r=0.5e−jΩ
- First Term a=1
Therefore Xa(Ω)=1−0.5ejΩ1
(b) xa[n]=n⋅0.5nu[n]
From Table, You can see this formula: Multiplication by n
nx[n]↔jdΩdX(Ω)
Basically, xb[n]=n⋅xa[n]
Therefore Xb(Ω)=jdΩdXa(Ω)
Do a differentiation.
Hint : f(x)=xr⟶f′(x)=rxr−1
Hint: Chain Rule
Hint: f(x)=eax⟶f′(x)=aeax
dΩdXa(Ω)=(−1)×(1−0.5e−jΩ)−2×(0−0.5×−je−jΩ)
=(−1)×(1−0.5e−jΩ)−2×(0.5je−jΩ)
= (1−0.5e−jΩ)2−j0.5e−jΩ
Xb(Ω)=jdΩdXa(Ω)=j(1−0.5e−jΩ)2−j0.5e−jΩ
Since j×−j=1
Xb(Ω)=(1−0.5e−jΩ)20.5e−jΩ

(a) v[n]=x[n−5]
From Table, you can see this formula: Time Shift
x[n−q]↔X(Ω)e−jqΩ,q is any integer
V(Ω)=X(Ω)⋅e−j5Ω=ejΩ+be−j5Ω
(b) v[n]=n⋅x[n]
From Table, You can see this formula: Multiplication by n
nx[n]↔jdΩdX(Ω)
V(Ω)=jdΩdX(Ω)=jdΩd(ejΩ+b1)
Do a differentiation.
Hint : f(x)=xr⟶f′(x)=rxr−1
Hint: Chain Rule
Hint: f(x)=eax⟶f′(x)=aeax
dΩd(ejΩ+b1)=dΩd(ejΩ+b)−1=(−1)×(ejΩ+b)−2×(jeΩ+0)=(ejΩ+b)2−jeΩ
Since j×−j=1
V(Ω)=j(ejΩ+b)2−jeΩ=(ejΩ+b)2ejΩ

(a) xc[n]=n⋅0.5n⋅cos(4n)⋅u[n]
xc[n]=n⋅0.5n⋅u[n]⋅cos(4n)
We break it into serval steps and store it with different variables.
Let y[n]=(0.5)nu[n]↔Y(Ω)=(1−0.5e−jΩ)1
Let z[n]=n⋅u[n]↔Z(Ω)=jdΩd(Y(Ω))=(1−0.5e−jΩ)20.5e−jΩ
xc[n]=z[n]cos(4n)↔Xc(Ω)=21[Z(Ω+4)+Z(Ω−4)]
Xc(Ω)=21⋅{(1−0.5e−j(Ω+4))20.5e−j(Ω+4)+(1−0.5e−j(Ω−4))20.5e−j(Ω−4)}
(b) xd[n]=(0.5)∣n∣−∞<n<∞
you need to know what it is exactly.

The first graph is how (0.5)∣n∣ looks like. (Not scaled to graph)
It is basically 0.5nu[n] + a flipped 0.5nu[n] - a overlapped pulse.
xd[n]=(0.5)∣n∣=(0.5)nu[n]+(0.5)−nu[−n]−δ[n]
Break it down into serveral steps.
Let f[n]=(0.5)nu[n]⟷F(Ω)=1−0.5e−jΩ1
f[−n]=(0.5)−nu[−n]⟷F(−Ω)=1−0.5ejΩ1
Therefore
xd[n]=f[n]+f[−n]−δ[n]⟷Xd(Ω)=F(Ω)+F(−Ω)−1
Xd(Ω)=1−0.5e−jΩ1+1−0.5ejΩ1−1
Do a simplification
Xd(Ω)=1−0.5e−jΩ1+1−0.5ejΩ0.5ejΩ=1−0.5e−jΩ−0.5ejΩ+0.251−0.5e−jΩ+0.5ejΩ−0.25=1.25−cosΩ0.75
Basically the hardest step is simplification -.-

(a) v[n]=x[n]−x[n−1]
V(Ω)=X(Ω)+X(Ω)e−jΩ=ejΩ+b1−ejΩ+be−jΩ
V(Ω)=ejΩ+b1⋅(1−e−jΩ)
(b) v[n]=x[n]⊗x[n]
V(Ω)=X(Ω)×X(Ω)=(eΩ−2+b)21
© v[n]=x[n]ej2n
V(Ω)=X(Ω−2)=eΩ−2+b1

(a) Obtain the 3 point DFT.
Forward DFT formula:
x[n]⟶X[k]=n=0∑N−1x[n]e−j2πNkn
Length = N=3
X[k]=∑n=03−1x[n]e−j2π3nk
X[k]=1×e−j2π30k+0×e−j2π31k+−1×e−j2π32k
X[k]=1−e−jπk34
X[0]=1−e−jπ34×0=1−1=0
X[1]=1−e−jπ34×1=1−(cos34π−jsin34π)=1.5−0.8666j=1.7321e−j0.5236
X[2]=1−e−jπ34×2=1−(cos38π−jsin38π)=1.5+0.8666j=1.7321ej0.5236
(b) Obtain the 6 point DFT.
Forward DFT formula:
x[n]⟶X[k]=n=0∑N−1x[n]e−j2πNkn
Length = N=6
X[k]=∑n=06−1x[n]e−j2π6nk
X[k]=1×e−j2π60k+0×e−j2π61k+−1×e−j2π62k
X[k]=1−e−jπk64=1−e−jπk32
X[0]=1−e−jπ32×0=1−1=0
X[1]=1−e−jπ32×1=1−(cos32π−jsin32π)=1.5+0.8666j=1.7321ej0.5236
X[2]=1−e−jπ32×2=1−(cos34π−jsin34π)=1.5−0.8666j=1.7321e−j0.5236
X[3]=1−e−jπ32×3=1−(cos2π−jsin2π)=0
X[4]=1−e−jπ32×4=1−(cos38π−jsin38π)=1.5+0.8666j=1.7321e−j0.5236
X[5]=1−e−jπ32×5=1−(cos310π−jsin310π)=1.5−0.8666j=1.7321e−j0.5236
©


4-point DFT equation:
X[k]=n=0∑3x[n]e−j2π4kn
(a) x[n] = [1 0 1 0]
X[k]=1+0+1×e−j2π42k+0=1+e−jπk
X[0]=1+1=2
X[1]=1+e−j1π=1−1=0
X[2]=1+e−j2π=1+1=2
X[3]=1+e−j3π=1−1=0
(b) x[n] = [1 0 -1 0]
X[k]=1+0+(−1)×e−j2π42k+0=1−e−jπk
X[0]=1−1=0
X[1]=1−e−j1π=1+1=2
X[2]=1−e−j2π=1−1=0
X[3]=1−e−j3π=1+1=2
© x[n] = [-1 0 1 2]
X[k]=−1+0+1×e−j2π42k+2×e−j2π43k=−1+e−jπk+2e−jπk23
X[0]=−1+1+2=2
X[1]=−1+e−j1π+2e−jπ23×1=−1−1+2j=−2+2j
X[2]=−1+e−j2π+2e−jπ23×2=−1+1+2e−j3π=−1+1−2=−2
X[3]=−1+e−j3π+2e−jπ23×3=−1−1+2(−j)=−2−2j
Discrete-time System Analysis via the DTFT and DFT
Recall: LTI System
linear time-invariant discrete-time systems (LTI system)
system outputs for a given input can be determined via a time domain system analysis
Output = input convolve with unit-pulse response
y[n]=i=0∑M−1h[i]x[n−i]
we can also determine the output via a frequency domain system analysis.
LTI system can respond to some basic input signals in frequency domain:
- Exponential input
- Cosine input
- Periodic input
- Aperiodic input
Discrete-time Signals
In frequency domain, DT signals are represented as
- Discrete time Fourier series
- Discrete time Fourier transform or Discrete Fourier transform
Frequency response (DTFT of h[n])
Tells how the system responds to individual frequency components of the input.
Basically = DTFT of h[n]
DTFT formula:
H(Ω)=i=−∞∑∞h[i]e−jΩi=i=0∑M−1h[i]e−jΩi
Recall :
You can get impulse response h[n] from the difference equation.
Then by changing the domain (Fouries Transform), you get H(ω).
Note:
ae−jkω↔aδ[n−k]
Learn to get common factors from ejω.
e−ajω+e−bjω=e2−a−b(e2∣−b+a∣+e2−∣−b+a∣)
- e.g. e−jω+e−2jω=e−1.5jω(e0.5jω+e−0.5jω)
(ea+e−a)=2cos(a)

x[n]=Aejϕejω^n
y[n]=H(ω^)Aejϕejω^n
where
H(Ω)=i=0∑M−1h[i]e−jΩi
^Frequency response of system
You need to know H(Ω) then you will be able to find y[n]
For LTI system with Exponential input:
- Frequencies of both Input & Output signals are ω^
- Frequency does not changed by the system!
- Output signal is
- the Input signal × the frequency response of H at frequency ω^
Reminder
Note:
You can get frequency response from impulse response h[n].
To know H(Ω)'s mag and phase:
H(Ω)=∣H(Ω)∣ej∠H(Ω)
mag = ∣H(Ω)∣
phase = ∠H(Ω)
ejΩ+e−jΩ=2cosΩ

In this case, x[n] is a periodic input. (cos input)
x[n]=A0+i=1∑NAicos(ω^in+ϕi)
y[n]=A0H(0)+i=1∑NAi∣H(ω^i)∣cos[ω^in+ϕi+∠H(ω^i)]
where
H(Ω)=i=0∑M−1h[i]e−jΩi
^Frequency response of system
You need to know H(Ω) then you will be able to find y[n]
For LTI system with Periodic input:
- Frequencies of both Input & Output signals are ω^i
- Frequency does not changed by the system!
- Output Amplitude scaled by the factor ∣H(ω^i)∣
- Output Phase shifted by ∠H(ω^i)

x[n]=N1k=0∑N−1X[k]ej2πNkn
y[n]=N1k=0∑N−1{X[k]H[k]}ej2πNk(n)
Note : N = Length of h[n] + Length of x[n] – 1
where
H[k]=n=0∑N−1h[n]e−j2πNkn
^Frequency response of system
You need to know H[k] and X[k] then you will be able to find y[n].
You use the same DFT formula to get X[k].
For LTI system with Periodic input:
- Identify N should be Length of h[n] + Length of x[n] - 1
- Get the DFT of the input first (X[k]) with N (use Zero Padding)
- Get the DFT of the impulse response (H[k]) with N (use Zero Padding)
- Then Multiply X[k] and H[k] to get Y[k]
- Output = Inverse DFT of X[k]H[k]
- N should be Length of h[n] + Length of x[n] - 1
- the length of the linear convolution output of h[n] and x[n]
or
- Get the convolution of x[n] and h[n] to get y[n] directly
Zero Padding
Assume missing samples are zeros.
Connection between DFT and Convolution
convolution in time domain = multiplication in frequency domain

Useful info
1↔δ[n]
ae−jkω↔aδ[n−k]
X(ω)↔ax[n−k]
H(−ω^)=H∗(ω^)
∣H(−ω^)∣=∣H(ω^)∣
∠H(−ω^)=−∠H(ω^)
ℜe{H(−ω^)}ℑm{H(−ω^)}=ℜe{H(ω^)}=−ℑm{H(ω^)}
Practice Questions - DFT and System

H(Ω)=k=−∞∑∞p2×4π(Ω+2πk)
Note:
H(Ω)↔h[n]
k=−∞∑∞p2B(Ω+2πk)↔πBsinc(πBn)
(a)
To get h[n]:
h[n]=π4πsinc(π4πn)
h[n]=41sinc(4n)
(b)
(i)
Find x[n]=cos(8nπ)
x[n] has 1 AC component which frequency is 8nπ
H(8nπ)=1 (See the H(Ω) graph)
y[n]=1×cos(8nπ+0)
=cos(8nπ)
(ii)
x[n]=cos(43nπ)+cos(16nπ)
H(43nπ)=0 (See the H(Ω) graph)
H(16nπ)=1 (See the H(Ω) graph)
y[n]=0cos(43πn+0)+1cos(16nπ+0)
=cos(16nπ)

Note :
δ[n]↔1
δ[n−N]↔e−jNΩ
(a)
h[n]=δ[n]+δ[n−1]+δ[n−2]+δ[n−3]
H(Ω)=1+e−j1Ω+e−j2Ω+e−j3Ω
=e−j0Ω+e−j1Ω+e−j2Ω+e−j3Ω
=e−jΩ(ejΩ+e−jΩ)+e−j2Ω(ejΩ+e−jΩ)
…
=4cos(Ω)cos(2Ω)e2−3jΩ
(b)
x[n]=4+3cos(0.2nπ+π/3)
x[n] has a DC component and a AC component which frequency is 0.2nπ
H(0)=4
H(0.2π)=3.077e2−3j0.2π=3.077e−0.3jπ
y[n]=4×4+3.077×3cos(0.2πn+3π−0.3π)
=16+9.233cos(0.2πn+3π−0.3π)

(a)
Fastest way: Factorize and do time-domain convolution
H(ω)=(1+e−jω)(1−ejπ/4e−jω)(1−e−jπ/4e−jω)
=(1+e−jω)(1−2cos(4ω)e−jω+e−2jω)
Now hop to
h[n]={1,1}⊗{1,−2,1}
h[n]={1,(1−2),(1−2),1}
h[n]=δ[n]+(1−2)δ[n−1]+(1−2)δ[n−2]+δ[n−3]















































