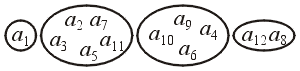Abstract Data Types and Data Relations
Abstract Data Types
https://ece.uwaterloo.ca/~dwharder/aads/Abstract_data_types/
An Abstract Data Type (ADT) is a way to define a set of objects together with a set of operations on them, without providing the implementation details
Examples of ADT: Set, List, Queue, Map, Graph
A ADT has:
- Data attributes
- Operations
Example:
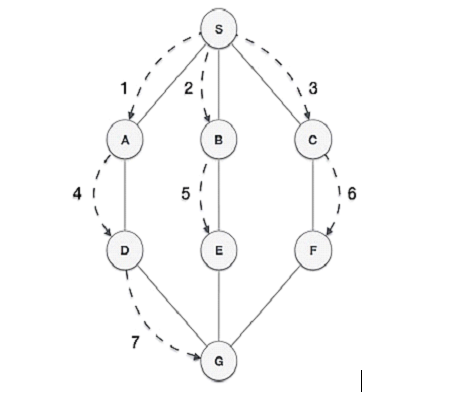
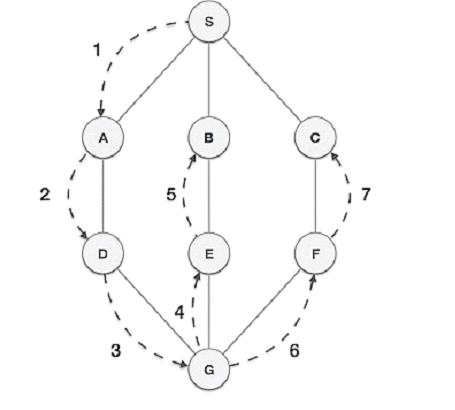
An undirected graph
Data attributes:
A set of nodes (coordinates (x, y))
A set of edges <v,v’> where v and v’ are nodes
Operations:
Create(G)
Insert(G, n)
Delete(G,k)
Shortest-Path(G, n, n’)
Data Relations
- Data relation is the basis of how efficient various operations on data objects would be
- The efficiency is both in terms of time and space
- Data relation can be non-existent (unlikely), in which case the data:
- We can choose a data structure that is most efficient in terms of time/space
Types of Data Relations
Symmetry
-
Symmetric
- if and only if
- example:
- Facebook friends (If A and B added friends, A is B’s friend and B is A’s friend).
-
Anti-symmetric
- if and then
- example:
- B is A’s mother but A is not B’s mother
Reflexivity
-
Reflexive
- for all
- example:
- A has same gender as A
-
Anti-reflexive
- for all
- example:
- A is not different gender than A
Transitivity
- Transitivity
- If and , then it must be true that
- example:
- If A has same age as B and B has same age as C, then A has same age as C.
Equivalence
- Happens if Symmetric. Reflexive and Transitive.
No Relation
The most generic ADT is a container (also called a dynamic set):
- Describes structures that store and give access to a set of objects
- There is no specific relation between the objects, except belonging to the container
Operations:
- Create/delete
- Insert/remove
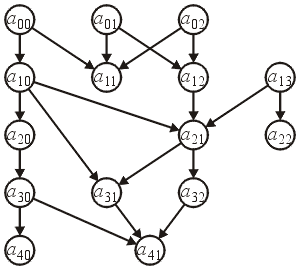
Adjacency Relations
The most generic relation between two data objects:
- a → b (read as a is adjacent to b) indicates that there is a direct connection from a to b.
an adjacency relation is explicitly defined by the programmer.
Example:
- Given two objects and in the container, are they connected? that is, is there a sequence of objects such that one can get from ?
- If the sequence exists, then there is a direct connection from a to b.
Equivalence Relations
A binary relationship a ~ b between two objects is said to be an equivalence relation iff
- The relationship is reflexive: Each object is related to itself: a ~ a
- The relationship is symmetric: a ~ b if and only if b ~ a
- The relationship is transitive: a ~ b and b ~ c implies that a ~ c
Partial Orderings
A partial ordering on a finite collection of objects may be described as follows:
- each object can have multiple immediate sucessors;
- however, it is not possible to start at a any object and following a path from that object to an immediate successor object and ultimately get back to the initial object—there are no loops.
- Properties:
-
Anti-symmetric
- if both and , it follows that
-
Transitive
- if and , this implies that
-
Partial Ordering is the best to implement a proof system (e.g. a SAT-solver).
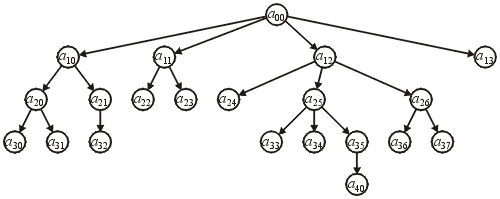
Hierarchical Orderings
A hierarchical ordering on a finite collection of objects may be described as follows:
- each object with exactly one exception has a parent object. The one exception is is an object which has no parent and this exception is called the root.
- All objects which have the same parent are said to be siblings and those objects are the children of the parent. An object with no children is said to be a leaf.
- Properties:
- Anti-symmetric
- if both and , it follows that
- Transitive
- if and , this implies that
- Anti-symmetric
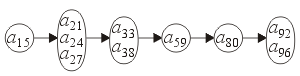
Linear Ordering
A linear ordering on a finite collection of objects may be described as follows:
- each object has exactly one immediate predecessor object and one immediate successor object with two exceptions: A first object has no predecessor and a last object has no successor.
- Any collection can be sorted according to this relation
- We could store linearly ordered sets using arrays or linked lists
- A linear ordering is any relationship where any two objects and that can be compared, exactly one of the conditions: is true and where the relation is transitive
Lexicographical Orderings
The order is determined by comparing the first letter/ element which differs (linear orderings for each element):
===
cd<ea===
cd<ch
Weak Orderings
- A weak ordering is a linear ordering of equivalence classes
A weak ordering on a finite collection of objects may be described as follows:
- the objects may be partitioned into classes such that all the objects in the same class are related and each class has exactly one immediate predecessor class and one immediate successor class with two exceptions: A first class has no predecessor and a last class has no successor.
Defining Relations
-
Implicit vs Explicit
- Integers are implicitly ordered based on their relative values
- Age groups are defined by the properties of the individuals
- A hierarchy in a company is explicitly defined
- The order of the letters on this slide is explicitly imposed by the author
-
Global vs Local
- Any two integers may be compared without reference to other integers
- Any two sets can be compared to determine if one is a subset of the other
C++ STL Data Structures
C++ STL: standard library that contains many packages including the implementation of various ADTs
- Containers: hash sets & maps
- Linear orderings: array, vector, list, stack, queue, priority queue
- Weak orderings: set, multiset, map, multimap
- STL containers: sets (with no keys), and maps (with key) containers
- Similar ones with no orderings are prefixed with unordered (e.g.,
unordered_set<type>)
Arrays
- An array is an ‘indexable continuous’ chunk of memory (linear ordering based on the address)
- Static array: the array is fixed size
- Dynamic array (vectors): the array size changes
- Operations: access, search, size/resize, insert, erase, push_back, pop_back
| Static Array | Dynamic Array | |
|---|---|---|
| Access | O(1) | O(1) |
| Search | O(n) | O(n) |
| Insertion | N/A | O(n) |
| Appending | N/A | O(1) |
| Deletion | N/A | O(n) |
List
- A list is a sequential set of nodes, each node has data and a link to the next/ previous node (non-continuous storage)
- The storage of a list is via storing the ‘head’ of the list
- Singly-linked list: only next node (last node is null)
- Doubly-linked list: both next and previous node (last node points to the first node)
- Operations: search, front, back, push_front, push_back, pop_front, pop_back, size
| Singly Linked | Doubly Linked | |
|---|---|---|
| Access | O(n) | O(n) |
| Search | O(1) | O(1) |
| Insertion | O(1) | O(1) |
| Appending | O(n) | O(n) |
| Deletion | O(n) | O(1) |
List vs Arrays:
- List has faster search, faster insertion
- Array has faster appending, faster access
Queue
- An interface to the sequence containers that creates two ends on the container, one for inserting and the other for removing elements (they can be defined based on FIFO)
- If the both ends take the order based on a given priority then we have priority queues
- Operations: insert (enqueue), remove (dequeue), size
Examples of queues applications: OS scheduler, graph breadth-first search (BFS)
- BFS wants FIFO

Stack
- An interface to the sequence containers that has only one end for inserting and removing elements (also called the top of the stack)
- Stack is also called a LIFO (Last-In-First-Out)
- Operations: push (insert), pop (remove), search, size
Examples of stacks applications: compilers for implementing function calls, graph depth-first search (DFS)