Tree

A tree is a frequently-used data structure to simulate a hierarchical tree structure.

It is already built into a lot of programming laguages.

What is a Tree?

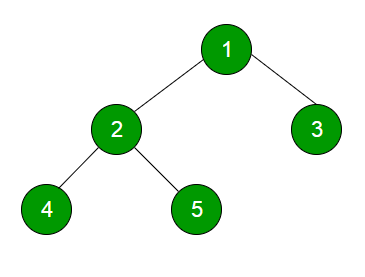
A tree is a collection of nodes.

Root - Node at the top of the tree
Child - Node below a given node connected by its edge downward
Parent - Any node which has one edge upward to a node. (except root node)
Leaf - Node which does not have any child
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
Subtree − Subtree represents the descendants of a node.

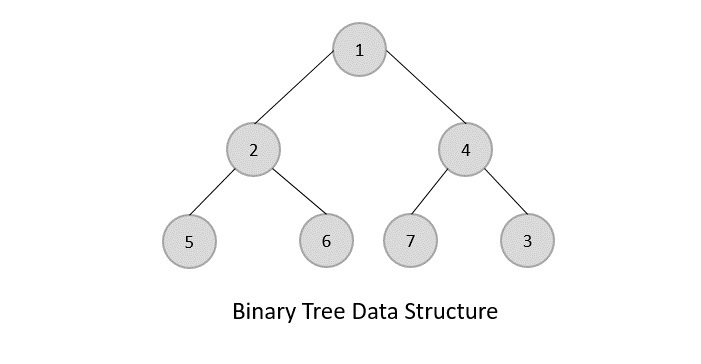
Binary Tree

A binary tree is a tree data stucture in which each node has at most two children, which are referred to as the left child and the right child.

Properties of Binary Tree

There are at most $2^{i-1}$ nodes on the i-th layer of the binary tree.
Binary Tree with depth k has at most $2^k-1$ nodes.
For any binary tree T, if the number of terminal nodes is $n$ and the number of nodes with degree 2 is $t$ , then $n=t+1$ .

Each Node at most two children

the two children are called the left child and the right child

Types of Binary Tree

Let’s pick some to explain.

Complete Binary Tree

Basically, a binary tree with all leaves have the same level.

Perfect Binary Tree

Basically, a binary tree with all interior nodes have two children and all leaves have the same level.

Balanced Binary Tree

Basically, Look like a tree.

Average case
Search in O( log(n) ) time
Insert in O( log(n) ) time

Degenerate Binary Tree (Unbalanced)

Basically, Look like a list. Only one child.

Worst case
Search in O(n) time (Linear)
Insert in O(n) time (Linear)

Binary Search Tree

Keypoint: Every round throw away half the numbers

Binary Search tree exhibits a special behavior. A node’s left child must have a value less than its parent’s value and the node’s right child must have a value greater than its parent value.

This ordering property makes finding a node very very fast because we have a pretty good idea of where it would be.

In each operation, we chopped off about half of the nodes.

For example, to find Node value contain 42, I just need to check is the value larger or smaller than the root? Then I choosed one side of nodes and that already ignored half of nodes in the tree and continue the operation. Now I need to check is the value larger or smaller than the 35? Yes it is, than I ingored another small half of nodes and found the Node value contain 42.

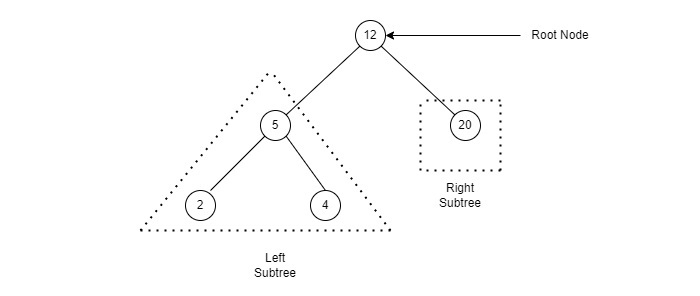
Properties of Binary Search Tree

left child value < parent value
right child value > parent value

Code Implementation

#include <iostream>
using namespace std;

struct node
{
  int data;
  // 1 node stick may stick with 2 child
  node* left;
  node* right;
};

node* createNode(int value) {
	node* newNode = new node;
  newNode->data = value;
  newNode->left = NULL;
  newNode->right = NULL;
  
  return newNode;
}

node* insert(node* root, int data)
{
	if (root == NULL)
    return createNode(data);
  
  if (data < root->data) // Note: left child value must be less than parent value
    root->left = insert(root->left, data); //recursive call
  else if (data > root->data)
    root->right = insert(root->right, data); //recursive call
  
  return root;
}

void inorder(node* root){
	if (root == NULL)
    return;
  inorder(root->left);
  cout << root->data << endl;
  inorder(root->right); 
}

int main(){
 	node *root = NULL;
  root = insert(root, 8);
  insert(root, 4);
  insert(root, 6);
  insert(root, 3);
  insert(root, 32);
  insert(root, 13);
  insert(root, 16);
  insert(root, 2);
  
  inorder(root);
}

Binary Tree Traversal

Binary Tree Traversing, also known as walking through a tree.

Let’s put a picture to confuse people here:

Inorder Traversal

Basically, Order: left -> root -> right

Typically in binary search trees we want to do inorder traversals because that actually allows the nodes to be printed in order.

^ Order: 1,2,3

Preorder Traversal

Basically, Order: root -> left -> right

In this traversal method, the root node is visited first, then the left subbtree and finally the right subtree.

Postorder Traversal

Basically, Order: **left -> right -> root **

In this traversal method, the left node is visited first, then the right subbtree and finally the root subtree.

Levelorder Traversal

Basically, Order: Starting from Level 0 (Left to Right)

In this traversal method, visit from the first level of the tree (root), then from the top to the bottom levels. If it is in the same level, the nodes are accessed one by one from the left to the right.